Joana
Finden Sie die von der X-Achse eingeschlossene Fläche und die Kurve Y=(x-4)(x-2)(x+2)?
1 Antworten
Hubertus
Die über der interessierenden Region eingeschlossene Fläche ist das eindeutige Integral dieses Ausdrucks über der interessierenden Region. Das Integral von
y = 16 - 4x - 4x^2 + x^3
ist
g[x] = Integral[y] = 16x - 2x^2 - (4x^3)/3 + x^4/4
Wenn der Bereich von Interesse ist x = {-2, 2}, die Fläche wird zu
g[2] - g[-2] = (52/3 - (-76/3)) = 128/3 ausgewertet.
Bitte schauen Sie sich das Bild an.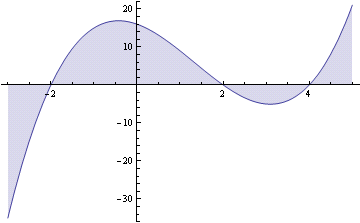
Verwandte Fragen
- Was ist die Mint-Paritätstheorie und wie wird ihre Rate bestimmt?
- Was meinst du mit Algorithmus und welchen Nutzen hat er in unserem täglichen Leben?
- Was ist Intervallskala und was sind die Eigenschaften dieser Skala?
- Was ist eine Verhältnisskala und wie hilft sie bei der Berechnung des Verhältnisses?
- X+2 geteilt durch X-Quadrat -8X +15.
- Was ist Verhältnisanalyse? Was sind seine Einschränkungen?
- Was ist Kointegration?
- Was ist Autokorrelation?