Как определить длину стороны правильного шестиугольника, если он занимает 10% бумаги 8,5x11?

Итак, предположим, что это был шестиугольник, который был на бумаге 8,5x11, и он покрыл 10% его:

Это будет означать, что площадь шестиугольника составляет 10% от площади бумаги 8,5x11, что также означает, что площадь бумаги в 10 раз больше площади шестиугольника. Для начала нам нужно рассчитать площади обеих фигур.

Площадь листа 8,5x11 должна соответствовать формуле для площади прямоугольника: длина, умноженная на ширину.

A (бумага) = 8,5 * 11 = 93,5 дюйма ^ 2.

Теперь у нас есть область бумаги. Напомним, что в задаче говорится, что шестиугольник покрывает 10% бумаги и, следовательно, занимает 1/10 площади бумаги. Так:

A (шестиугольник) = A (бумага) / 10

Мы уже знаем, какова площадь бумаги.

A (шестиугольник) = 93,5 / 10

= 9,35 дюйма ^ 2

Теперь мы знаем площади обеих фигур и должны выяснить, каковы длины сторон. Согласны ли вы, что шестиугольник выглядит как 6 равносторонних треугольников вместе взятых? Взгляните на это:

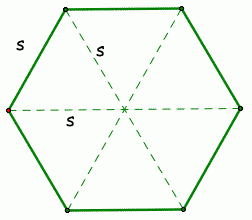
Пока не обращайте внимания на символы "s".

Напомним, что площадь равностороннего треугольника равна основанию, умноженному на высоту, деленному на 2.

А (треугольник) = bh / 2

Однако в этом шестиугольнике таких треугольников шесть. Мы можем использовать площадь шестиугольника, чтобы найти площадь только одного равностороннего треугольника, и умножить ее на 6, а затем узнать длины наших сторон.

A (треугольник) = A (шестиугольник) / 6

А (треугольник) = 9,35 / 6

A (треугольник) = bh / 2 = 1,558 дюйма ^ 2 (примерно столько)

С этого момента потребуется немного тригонометрии с использованием прямоугольных треугольников.

Предполагалось, что это будет равносторонний треугольник, но я как бы быстро нарисовал его, так что простите за мои плохие навыки художника.

Так или иначе, я нарисовал линию в середине треугольника, которая представляет высоту. Но пока забудьте об этом. В тригонометрии всякий раз, когда возникает такая форма с линией по центру, всегда будет угол 30, 60 и 90 градусов. Я пометил это на фигуре. А для сторон, противоположных углу, они представляли некоторую длину.

Углы 30 градусов обозначаются буквой «а».

Углы 60 градусов представлены как "a", умноженное на "sqrt (3)".

Углы в 90 градусов представлены как "a", умноженное на 2.

Вернемся к линии по центру треугольника. Это означает высоту, как я упоминал ранее. Но знаете что? Он также представляет собой * sqrt (3). Таким образом, мы можем использовать это значение в качестве значения высоты в нашем уравнении для треугольника.

A (треугольник) = 1,558 = [b * a * sqrt (3)] / 2

Теперь найти б. Обратите внимание, что буква «a», противоположная углу в 30 градусов, представляет только левую половину длины стороны основания. Поскольку он измеряет только половину, мы должны умножить его на 2, чтобы получить длину всего основания треугольника, что составит 2a. Итак, b = 2a.

A (треугольник) = 1,558 = [2a * a * sqrt (3)] / 2

Поверьте, отсюда станет НАМНОГО проще. Упростите уравнение, чтобы найти a.

1,558 = [2a ^ 2 * sqrt (3)] / 2

1.558 = a ^ 2 * sqrt (3) (2 перед a ^ 2 отменяются, а 2 делит всю правую часть уравнения)

1,558 / sqrt (3) = a ^ 2

а ^ 2 = 0,9

Извлеките квадратный корень из обеих частей.

а = 0,948

Теперь, когда мы знаем, что такое a, давайте вернемся немного назад. Как мы уже говорили ранее, b = 2a, верно? Ну, угадайте, что тоже обозначает b? Длина стороны шестиугольника!

Да, это длина стороны равностороннего треугольника, но шестиугольник состоит из 6 равносторонних треугольников, поэтому у них обоих будут одинаковые длины сторон.

Длина стороны = 2a

Вставьте значение для.

Длина стороны = 2 (0,948) = 1,896 дюйма