Если две вершины равностороннего треугольника - это (-4, -3) и (4, 1), найти оставшуюся вершину?

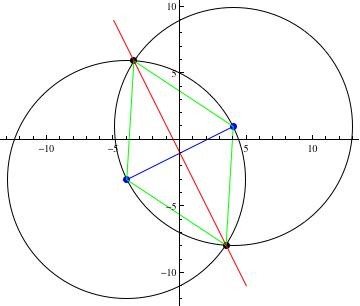
Таких вершин будет две. Один будет во втором квадранте, а один - в четвертом. Они будут лежать на серединном перпендикуляре линии между данными точками, и они будут найдены в точках пересечения кругов с центром в каждой точке, имеющей радиус, равный расстоянию между точками. (См. Рисунок ниже.)

Расстояние между данными точками равно
  r = √ ((- 4-4) ^ 2 + (-3-1) ^ 2) = √ (64 + 16) = √80

Круг с центром at (-4, -3) имеет уравнение
  (x + 4) ^ 2 + (y + 3) ^ 2 = 80
  x ^ 2 + 8x + 16 + y ^ 2 + 6y + 9 = 80 (расширение уравнения. Назовите это [1])

Круг с центром в точке (4, 1) имеет уравнение
  (x - 4) ^ 2 + (y - 1) ^ 2 = 80
  x ^ 2 - 8x + 16 + y ^ 2 - 2y + 1 = 80 (расширение уравнения. Назовите это [2]).

Мы можем установить [1] = [2] и решить относительно y.
  x ^ 2 + 8x + 16 + y ^ 2 + 6y + 9 = 80 = x ^ 2 - 8x + 16 + y ^ 2 - 2y + 1
  8x + 6y + 9 = -8x - 2y + 1 (вычесть x ^ 2 + 16 + y ^ 2 с обеих сторон)
  6y = -16x - 2y - 8 (вычесть 8x + 9 с обеих сторон)
  8y = -16x - 8 (добавить 2y)
  y = -2x - 1 (разделить на 8. Это уравнение красной линии (назовем это [3])

Мы можем подставить [3] в [1] и решить относительно x. На рисунке это дает координату x точек пересечения красной линии и нижнего круга.
  х ^ 2 + 8x + 16 + ( -2x - 1 ) ^ 2 + 6 ( -2x - 1 ) + 9 = 80
  x ^ 2 + 8x + 16 + 4x ^ 2 + 4x + 1 - 12x - 6 + 9 = 80 (исключить скобки)
  5x ^ 2 + 20 = 80 (собрать члены)
  5x ^ 2 = 60 (вычесть 20)
  x ^ 2 = 12 (разделить на 5)
  x = ± 2√3     (извлечь квадратный корень)

Мы можем использовать этот результат в [3], чтобы найти соответствующие значения y. (Сначала положительный знак.)
  Y = -2 (2√3) - 1 = -4√ (3) - 1
Вершина квадранта IV равна (2√3, -4√ (3) - 1) .

  y = -2 (-2√3) - 1 = 4√ (3) - 1
Вершина квадранта II равна (-2√3, 4√ (3) - 1) .