Si deux sommets d'un triangle équilatéral sont (-4, -3) et (4, 1), trouvez le sommet restant ?

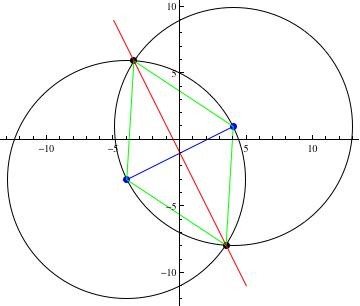
Il y aura deux de ces sommets. L'un sera dans le deuxième quadrant et l'autre dans le quatrième quadrant. Ils se situeront sur la médiatrice de la ligne entre les points donnés, et ils se trouveront aux points d'intersection de cercles centrés en chaque point ayant un rayon égal à la distance entre les points. (Reportez-vous à la figure ci-dessous.)

La distance entre les points donnés est
  r = √((-4-4)^2 + (-3-1)^2) = √(64+16) = √80

Le cercle centré à (-4, -3) a l'équation
  (x + 4)^2 + (y + 3)^2 = 80
  x^2 + 8x + 16 + y^2 + 6y + 9 = 80 (développement de l'équation. Appelez ceci [1])

Le cercle centré en (4, 1) a l'équation
  (x - 4)^2 + (y - 1)^2 = 80
  x^2 - 8x + 16 + y^2 - 2y + 1 = 80 (développement de l'équation. Appelons ceci [2])

Nous pouvons définir [1] = [2] et résoudre pour y.
  x^2 + 8x + 16 + y^2 + 6y + 9 = 80 = x^2 - 8x + 16 + y^2 - 2y + 1
  8x + 6y + 9 = -8x - 2y + 1 (soustraire x^2 +16+y^2 des deux côtés)
  6y = -16x - 2y - 8 (soustrayez 8x+9 des deux côtés)
  8y = -16x - 8 (ajoutez 2y)
  y = -2x - 1 (divisez par 8. C'est l'équation de la ligne rouge.Appelez ceci [3])

Nous pouvons substituer [3] dans [1] et résoudre pour x. Sur la figure, cela donne la coordonnée x des points d'intersection de la ligne rouge et du cercle inférieur.
  x^2 + 8x + 16 + ( -2x - 1 )^2 + 6( -2x - 1 ) + 9 = 80
  x^2 + 8x + 16 + 4x^2 + 4x + 1 - 12x - 6 + 9 = 80 (supprimer les parenthèses)
  5x^2 + 20 = 80 (collecter les termes)
  5x^2 = 60 (soustraire 20)
  x^2 = 12 (diviser par 5)
  x = ±2√3     (prendre la racine carrée)

Nous pouvons utiliser ce résultat dans [3] pour trouver les valeurs correspondantes de y. (Signe positif en premier.)
  y = -2(2√3) - 1 = -4√(3) - 1
Le sommet du quadrant IV est (2√3, -4√(3) - 1) .

  y = -2(-2√3) - 1 = 4√(3) - 1
Le sommet du quadrant II est (-2√3, 4√(3) - 1) .