Comment trouvez-vous les longueurs de côté d'un hexagone régulier s'il occupe 10% d'un papier 8.5x11 ?
1 Réponses
Adolphe
Alors disons que c'était l'hexagone qui était sur un papier 8.5x11 et qu'il en couvrait 10 % :
Cela signifierait que la surface de l'hexagone est de 10 % la surface d'un papier 8,5 x 11, ce qui signifie également que la surface du papier est 10 fois plus grande que celle de l'hexagone. Nous devons commencer par calculer les aires des deux formes.
L'aire d'un papier 8.5x11 doit utiliser la formule pour l'aire d'un rectangle : Longueur fois largeur.
A(papier) = 8,5 * 11 = 93,5 po^2.
Nous avons maintenant la zone du papier. Rappelons que le problème indique que l'hexagone couvre 10 % du papier, et a donc 1/10 de la surface du papier. Alors:
A(hexagone) = A(papier)/10
Nous savons déjà quelle est la surface du papier.
A(hexagone) = 93,5/10
= 9,35 po.^2
Maintenant, nous connaissons les zones des deux formes et devons déterminer quelles sont les longueurs des côtés. Seriez-vous d'accord pour dire qu'un hexagone ressemble à 6 triangles équilatéraux combinés ? Regarde ça:
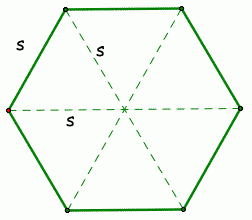
Ignorez les symboles "s" pour le moment.
Rappelons que l'aire d'un triangle équilatéral est la base multipliée par la hauteur divisée par 2.
A(triangle) = bh/2
Cependant, dans cet hexagone, nous avons six de ces triangles. Nous pouvons utiliser l'aire de l'hexagone pour trouver l'aire d'un seul triangle équilatéral et la multiplier par 6, puis trouver nos longueurs de côté.
A(triangle) = A(hexagone)/6
A(triangle) = 9,35/6
A(triangle) = bh/2 = 1,558 in.^2 (environ autant)
À partir de ce point, un peu de trigonométrie va être impliqué en utilisant des triangles rectangles.
C'était censé être un triangle équilatéral, mais je l'ai un peu dessiné rapidement, alors pardonnez mes mauvaises compétences d'artiste.
Quoi qu'il en soit, j'ai tracé une ligne au milieu du triangle, qui représente la hauteur. Mais oubliez ça pour le moment. En trigonométrie, chaque fois qu'une forme comme celle-ci se produisait, avec une ligne au centre, il y aurait toujours un angle de 30, 60 et 90 degrés. Je l'ai marqué sur la forme. Et pour les côtés opposés à l'angle, ils représentaient une certaine longueur.
Les angles de 30 degrés sont représentés par "a".
Les angles de 60 degrés sont représentés par "a" multiplié par "sqrt(3)".
Les angles de 90 degrés sont représentés par "a" multiplié par 2.
Revenons à la ligne au centre du triangle. Cela représente la hauteur, comme je l'ai déjà mentionné. Mais devinez quoi ? Il représente également un * sqrt(3). Nous pouvons donc l'utiliser comme valeur de hauteur dans notre équation pour le triangle.
A(triangle) = 1,558 = [b * a * sqrt(3)]/2
Maintenant pour trouver b. Remarquez comment "a", qui est opposé à l'angle de 30 degrés, ne représente que la moitié gauche de la longueur du côté de la base. Puisqu'il ne mesure que la moitié, nous devons le multiplier par 2 pour nous donner la longueur de toute la base du triangle, ce qui en fera 2a. Donc b = 2a.
A(triangle) = 1.558 = [2a * a * sqrt(3)]/2
Cela devient BEAUCOUP plus facile à partir d'ici, croyez-moi. Simplifier l'équation à résoudre pour a.
1,558 = [2a^2 * carré(3)]/2
1.558 = a^2 * sqrt(3) (le 2 devant a^2 s'annule avec le 2 divisant tout le côté droit de l'équation)
1.558/sqrt(3) = a^2
a^2 = 0.9
Prenez la racine carrée des deux côtés.
a = 0,948
Maintenant que nous savons ce qu'est un, revenons un peu en arrière. Comme nous l'avons dit plus tôt, b = 2a, n'est-ce pas ? Eh bien, devinez ce que b représente aussi ? La longueur de côté d'un hexagone !
Oui, c'est une longueur de côté du triangle équilatéral, mais un hexagone est composé de 6 triangles équilatéraux, ils auront donc tous les deux la même longueur de côté.
Longueur côté = 2a
Branchez la valeur pour a.
Longueur latérale = 2 (0,948) = 1,896 po.
Questions connexes
- Comment calculer le volume d'un cylindre ?
- Qu'est-ce qu'un polyèdre?
- Combien de côtés a un polygone ?
- Quels sont les angles d'un octogone ?
- Quelle est la mesure d'un angle extérieur ?
- Pourquoi un trou d'homme est-il en forme de cercle uniquement ?
- Que signifie la géométrie ?
- Que signifie quadrilatère ?