Jude
Comment trouver le degré d'un triangle en utilisant la trigonométrie ?
17 Réponses
Blaise
J'ai besoin d'une formule pour calculer les dimensions de 2 côtés d'un triangle. Je connais les degrés des 3 côtés du triangle. 90, 30, 60. L'hypoténuse est de 36".
Aidez-moi s'il vous plaît ! Quelqu'un ?Beulah
Si le premier angle est x le
deuxième angle est 2x le
3ème angle est ???
Et les trois angles doivent s'additionner au total de tous les angles de tous les trianglesHarmonie
Le deuxième angle d'un triangle est supérieur de 15 degrés au premier. Le troisième angle est inférieur de 23 degrés au premier. Quelle est la mesure exacte des trois angles. AiderKatrine
Eh bien, disons que vous avez 40 et 50, puis vous les additionnez et la réponse serait 90 pour la dernière étape, puis vous soustrayez 90 de 180 et 180 car 180 est la longueur des triangles quoi qu'il arrive !Sandrine
Eh bien, vous devez savoir quel est l'angle d'un triangle plein. Ensuite, déterminez la quantité de triangle manquante. Vous pouvez soustraire ces deux pour savoir quelle quantité d'angle du triangle est réellement là aussi en utilisant cette méthode.Philippe
180 degrés équivaut à un triangle. Si un angle est de 30, disons et un autre est de 70, en faisant semblant, alors que faut-il de plus pour égaler 180 ? Dans ce faux cas, ce serait 80, ce qui signifierait que l'angle restant est de 80 degrés.Frieda
Utilisez la formule a+b+c=180 degrés J'avais la même question et c'est ce que mon professeur m'a dit. Cela fonctionne vraiment, je peux le garantir!Elliott
Vous prenez le nombre d'angle le plus élevé et soustrayez le nombre le plus bas du nombre le plus élevé, votre réponse est donc celle que vous avez soustraite !!! Est-ce que c'était facile ?Dedrick
Comment trouver les angles manquants d'un triangle avec un seul angle donné ; la base est de 16" et la hauteur est de 4"Kacié
La mesure du deuxième angle d'un triangle est de 5 degrés de plus de 4 fois celle du premier, et la mesure du troisième angle est de 27 degrés de moins de trois fois celle du deuxième angle. Trouvez la mesure de chaque angle.Haley
Vous pouvez à peu près calculer n'importe quel angle en utilisant des fonctions trigonométriques. Ces fonctions fonctionnent avec des triangles rectangles mais fourniront des réponses pour tout triangle pouvant être divisé en deux triangles rectangles.
Étant donné l'illustration :
Le sinus de l'angle a est le rapport de la longueur du côté opposé à la longueur de l'hypoténuse.
Le cosinus de l'angle a est le rapport de la longueur du côté adjacent à la longueur de l'hypoténuse.
La tangente de l'angle a est le rapport de la longueur du côté opposé à la longueur du côté adjacent.
Juste au cas où vous ne le sauriez pas, le rapport signifie divisé par.
Connaissant la longueur des deux côtés du triangle, nous pouvons calculer soit le sinus, le cosinus ou la tangente et à partir de cela déterminer l'angle.
Puisque la somme des trois angles d'un triangle doit être de 180 o et qu'un angle d'un triangle rectangle est toujours de 90 o, nous pouvons calculer le troisième angle.
À titre d'exemple, supposons que le côté adjacent soit de 6 pouces et que l'hypoténuse soit de 8 pouces, nous pouvons calculer le cosinus de l'angle a comme 6/8 = 0,750 . Si nous vérifions les tables de trig ou une calculatrice sophistiquée, nous voyons que 0,750 est le cosinus de l'angle 41,41 o . Si vous n'avez pas de calculatrice sophistiquée et que vous utilisez les tableaux, vous devrez peut-être interpoler. (Mais c'est une autre histoire).
Étant donné que l'angle inconnu = 180-(90+41,41), les trois angles sont 41,41, 90 et 48,59.
Il existe d'autres fonctions trignométriques, mais le sinus, le cosinus et la tangente feront le gros du travail.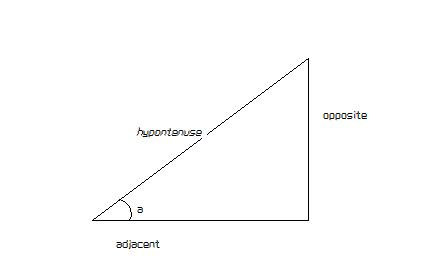
Il y a un
Les trois angles sont
x
2x
2x + 10
Ils doivent totaliser 180
x + 2x + 2x + 10 = 180
5x + 10 = 180
5x = 170
x = 34 (angle1
2x = 68(angle2)
y=2x+10
y = 2(34) + 10
y = 78 (angle3)
34 + 68 + 78 = 180.
Nédra
Tous les angles d'un triangle totalisent 180 degrés, quelle que soit la taille du triangle, disons qu'un angle fait 50 degrés, un autre 50 degrés, puis quel est le dernier 1 ? Il devrait faire 80 degrés --- 50+50+_=180 ? 50+50+80=180.Kadin
Normalement dans n'importe quel triangle, la somme des trois angles est de 180. Vous connaissez déjà deux angles. Vous devez trouver l'angle manquant. Considérons le triangle ABC. Dans ce triangle A, B sont les angles connus. Nous devons trouver l'angle C. la somme des trois angles est 180. donc, A+B+C = 180, C = 180 - (A+B)Filiberto
Vous allez toujours avoir une longueur de 180 pour votre triangle et quand vous savez que tout découle de là, parce que disons que vos deux autres angles sont 30 et 20 ce qui vous donne 50 alors vous soustrayez 50 de 180 et obtenez 130 qui sera votre manquant angle, j'espère que cela aide de quelque façon :)Ewald
Il existe des formules que vous pouvez utiliser pour calculer les degrés d'un triangle à l'aide de la trigonométrie.
A=angle 1
b = angle 2
c = angle 3
A = côté 1
B = côté 2
C = côté 3
a² = b²+c² - 2bc car A
c² = a² + b² - 2ab car C
Sin A/a =Sin C/ c = Sin B/b
Adjacent signifie à côté ou côte à côte. Comme des angles adjacents ou des côtés adjacents. L'hypoténuse est le côté opposé d'un angle de 90 degrés dans un triangle rectangle. Comme , si vous tracez deux lignes à angle droit, la troisième ligne qui relie les deux sera l'hyponténuse.Alec
Vous additionnez les angles donnés et soustrayez la somme de ces deux nombres de 180 degrés car peu importe ce que le triangle additionnera jusqu'à 180... Et quelle que soit la réponse que vous obtenez, c'est le nombre de degrés manquants.
Et puis c'est fait.
J'espère que cela a aidé.
Questions connexes
- Comment calculer le volume d'un cylindre ?
- Qu'est-ce qu'un polyèdre?
- Combien de côtés a un polygone ?
- Quels sont les angles d'un octogone ?
- Quelle est la mesure d'un angle extérieur ?
- Pourquoi un trou d'homme est-il en forme de cercle uniquement ?
- Que signifie la géométrie ?
- Que signifie quadrilatère ?