Explica por qué crees que los pares de ángulos formados por dos líneas y una transversal están relacionados. ¿Por qué podría ser útil identificarlos como ángulos que van juntos en lugar de ángulos independientes?

Están relacionados de muchas formas.

Se necesita una transversal para formar pares de ángulos, como en esta imagen.

La transversal es claramente la línea que es mayoritariamente vertical, en comparación con las otras dos líneas. Sin él, no se podrían formar pares de ángulos. Sin embargo, todavía se pueden hacer sin una transversal, como en esta imagen.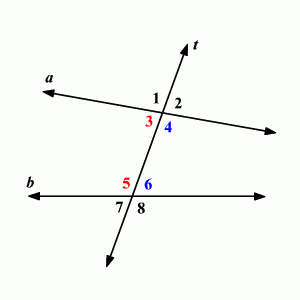

Sin embargo, la imagen 1 muestra más de cómo una transversal se relaciona con los pares de ángulos, ¡porque es necesaria para hacerlos!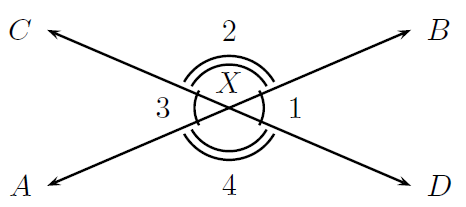

¿Por qué podría ser útil identificarlos como ángulos que van juntos en lugar de ángulos independientes?

Echemos un vistazo a la segunda imagen. Muestra que los ángulos 1 y 3 son iguales (dibujando un arco pequeño al lado de cada ángulo), así como los ángulos 2 y 4 son iguales (dibujando dos arcos pequeños al lado de cada ángulo). Si nos pidieran que averigüáramos la medida exacta del grado de los ángulos, usar pares de ángulos aquí nos ahorraría el 50% del trabajo. Digamos que averiguamos la medida en grados para el ángulo 1. Debido a una regla de pares de ángulos, podemos decir que el ángulo 3 tiene la misma cantidad de grados, lo que ya nos ahorra un 25% del trabajo total. Si hacemos lo mismo en los ángulos 2 y 4, se ahorrará otro 25% del trabajo total. Por eso es útil identificar los pares de ángulos como ángulos que van juntos en lugar de ángulos independientes.

Una transversal es una sola línea que cruza dos o más líneas. Estas líneas pueden ser paralelas pero no es necesario que lo sean. Este es uno de los conceptos fundamentales de la geometría.

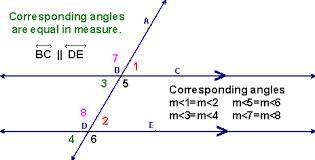
La transversal crea un ángulo a partir de lo que de otro modo sería esencialmente dos líneas rectas. Cuando esto sucede, los ángulos formados se dividen en pares: ángulos verticales, ángulos correspondientes, ángulos alternos internos, alternos externos y consecutivos ángulos internos.

La única otra forma en que dos líneas rectas podrían formar ángulos sin la ayuda de una transversal es si las dos líneas se cruzan en algún punto.

Es útil identificar los ángulos en pares, en lugar de de forma independiente, porque sabemos que un grupo de ángulos creado por una transversal comparte propiedades que facilitan su identificación. Por ejemplo, los dos ángulos 7 y 1 en la imagen de arriba, juntos forman una línea recta, lo que nos dice que la suma de sus medidas debe ser de 180 grados.