¿Cuál es la medida del ángulo de abolladura de un polígono en forma de estrella con 8 puntos y un ángulo de 200?

Suponiendo un polígono regular que consta de 8 puntos y 8 "abolladuras", la figura parecería ser una de las siguientes. (El ángulo de 200 ° está marcado con un arco).
De cualquier manera, la "abolladura" parece parecerse mucho a un "punto".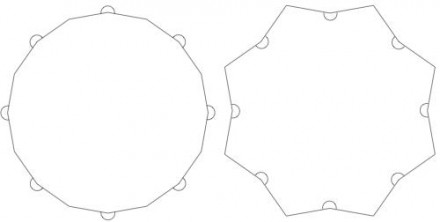
Si las abolladuras y los puntos se miden como ángulos internos (como a la derecha), la suma de un par de abolladuras y puntos será 14/8 * 180 ° = 315 °. Por lo tanto, un ángulo de "abolladura" será de 115 °.
Si las abolladuras y los puntos se miden en el exterior (como a la izquierda), la suma correspondiente de cada par de abolladuras y puntos será 360 ° (1 + 1/8) = 405 °. Por tanto, un ángulo de "abolladura" será de 205 °.
Por supuesto, el ángulo cóncavo en la figura de la derecha es 360 ° - 200 ° = 160 °.

Quizás te refieres a que el ángulo de la punta es de 20 °. Entonces la figura se vería así.
El ángulo de "abolladura" interior es de 315 ° - 20 ° = 295 °, por lo que el ángulo de abolladura exterior es de 65 ° .