¿Cómo se encuentran las longitudes de los lados de un hexágono regular si ocupa el 10% de un papel de 8.5x11?

Entonces, digamos que este era el hexágono que estaba en un papel de 8.5x11 y cubría el 10%:

Eso significaría que el área del hexágono es un 10% del área de un papel de 8.5x11, lo que también significa que el área del papel es 10 veces mayor que la del hexágono. Necesitamos calcular las áreas de ambas formas para empezar.

El área de un papel de 8.5x11 debe usar la fórmula para el área de un rectángulo: Largo por ancho.

A (papel) = 8.5 * 11 = 93.5 pulg. ^ 2.

Ahora tenemos el área del papel. Recuerde que el problema establece que el hexágono cubre el 10% del papel y, por lo tanto, tiene 1/10 del área del papel. Entonces:

A (hexágono) = A (papel) / 10

Ya sabemos cuál es el área del papel.

A (hexágono) = 93,5 / 10

= 9,35 pulg. ^ 2

Ahora conocemos las áreas de ambas formas y debemos averiguar cuáles son las longitudes de los lados. ¿Estarías de acuerdo en que un hexágono se parece a 6 triángulos equiláteros combinados? Mira esto:

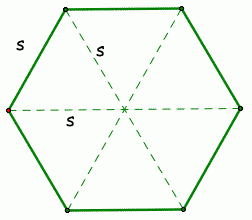
Ignore los símbolos "s" por el momento.

Recuerda que el área de un triángulo equilátero es la base por la altura dividida por 2.

A (triángulo) = bh / 2

Sin embargo, en este hexágono, tenemos seis de estos triángulos. Podemos usar el área del hexágono para encontrar el área de un solo triángulo equilátero y multiplicar eso por 6, y luego encontrar las longitudes de nuestros lados.

A (triángulo) = A (hexágono) / 6

A (triángulo) = 9.35 / 6

A (triángulo) = bh / 2 = 1,558 pulg. ^ 2 (alrededor de esa cantidad)

A partir de este punto, se involucrará un poco de trigonometría usando triángulos rectángulos.

Se suponía que esto era un triángulo equilátero, pero lo dibujé un poco rápido, así que perdona mis malas habilidades como artista.

De todos modos, dibujé una línea en el medio del triángulo, que representa la altura. Pero olvídate de eso por ahora. En trigonometría, siempre que ocurra una forma como esta, con una línea en el centro, siempre habrá un ángulo de 30, 60 y 90 grados. Lo etiqueté en la forma. Y para los lados opuestos al ángulo, representaron cierta longitud.

Los ángulos de 30 grados se representan como "a".

Los ángulos de 60 grados se representan como "a" multiplicado por "sqrt (3)".

Los ángulos de 90 grados se representan como "a" multiplicado por 2.

Volvamos a la línea del centro del triángulo. Eso representa la altura, como mencioné antes. ¿Pero adivina que? También representa una * sqrt (3). Entonces podemos usar esto como el valor de la altura en nuestra ecuación para el triángulo.

A (triángulo) = 1,558 = [b * a * sqrt (3)] / 2

Ahora para encontrar b. Observe cómo "a", que es opuesto al ángulo de 30 grados, representa solo la mitad izquierda de la longitud lateral de la base. Como mide solo la mitad, tenemos que multiplicarlo por 2 para darnos la longitud de toda la base del triángulo, lo que lo convertirá en 2a. Entonces b = 2a.

A (triángulo) = 1.558 = [2a * a * sqrt (3)] / 2

Se vuelve MUCHO más fácil desde aquí, créeme. Simplifica la ecuación para resolver a.

1,558 = [2a ^ 2 * sqrt (3)] / 2

1.558 = a ^ 2 * sqrt (3) (el 2 frente al a ^ 2 se cancela con el 2 dividiendo todo el lado derecho de la ecuación)

1.558 / raíz cuadrada (3) = a ^ 2

a ^ 2 = 0,9

Saca la raíz cuadrada de ambos lados.

a = 0,948

Ahora que sabemos qué es a, retrocedamos un poco. Como dijimos antes, b = 2a, ¿verdad? Bueno, ¿adivinen qué representa también b? ¡La longitud lateral de un hexágono!

Sí, es una longitud de lado del triángulo equilátero, pero un hexágono está formado por 6 triángulos equiláteros, por lo que ambos tendrán la misma longitud de lado.

Longitud lateral = 2a

Ingrese el valor de a.

Longitud de lado = 2 (0,948) = 1,896 pulg.