Judas
¿Cómo se encuentra el grado de un triángulo mediante trigonometría?
17 Respuestas
Blaise
Necesito una fórmula para calcular las dimensiones de 2 lados de un triángulo. Conozco los grados de los 3 lados del triángulo. 90, 30, 60. La hipotenusa es 36 ". ¡
Por favor ayuda! ¿Alguien?Beulah
Si el primer ángulo es x el
segundo ángulo es 2x, el
tercer ángulo es ???
Y los tres ángulos deben sumar el total de todos los ángulos de todos los triángulosArmonía
El segundo ángulo de un triángulo es 15 grados más que el primero. El tercer ángulo es 23 grados menos que el primero. ¿Cuál es la medida exacta de los tres ángulos? AyudarKatrine
Bueno, digamos que tiene 40 y 50, luego los suma y la respuesta sería 90 para el último paso, luego resta 90 de 180 y 180 porque 180 es la longitud de los triángulos sin importar qué.Sandrine
Bueno, necesitas saber cuál es el ángulo de un triángulo completo. Luego, averigua cuánto del triángulo falta. Puede restar esos dos para averiguar cuánto del ángulo del triángulo está realmente allí también usando ese método.Felipe
180 grados es igual a un triángulo. Si un ángulo es 30, digamos y otro es 70, fingiendo, entonces ¿qué más se necesita para igualar 180? En este caso falso, sería 80, lo que significaría que el ángulo restante es de 80 grados.Frieda
Use la fórmula a + b + c = 180 grados. Tenía la misma pregunta y esto es lo que me dijo mi maestro. Realmente funciona, ¡puedo garantizarlo!Elliott
¡¡¡Toma el número de ángulo más alto y resta el número más bajo del más alto, por lo que tu respuesta es la respuesta que hayas restado !!! ¿Qué tan fácil fue eso?Dedrick
¿Cómo se encuentran los ángulos faltantes de un triángulo con un solo ángulo dado? la base es de 16 "y la altura es de 4"Kacie
La medida del segundo ángulo de un triángulo es 5 grados más que 4 veces la del primero, y la medida del tercer ángulo es 27 grados menos que tres veces la del segundo ángulo. Encuentre la medida de cada ángulo.Haley
Puedes calcular prácticamente cualquier ángulo usando funciones trigonométricas. Estas funciones funcionan con triángulos rectángulos, pero proporcionarán respuestas para cualquier triángulo que se pueda dividir en dos triángulos rectángulos.
Dada la ilustración:
el seno del ángulo a es una razón entre la longitud del lado opuesto y la longitud de la hipotenusa.
El coseno del ángulo a es una razón entre la longitud del lado adyacente y la longitud de la hipotenusa.
La tangente del ángulo a es una relación entre la longitud del lado opuesto y la longitud del lado adyacente.
En caso de que no sepa la razón significa dividida por.
Al conocer la longitud de dos lados cualesquiera del triángulo, podemos calcular el seno, el coseno o la tangente y, a partir de ahí, determinar el ángulo.
Dado que la suma de los tres ángulos de un triángulo debe ser 180 ° y un ángulo de un triángulo rectángulo es siempre 90 ° , podemos calcular el tercer ángulo.
Como ejemplo, suponga que el lado adyacente mide 6 pulgadas y la hipotenusa es 8 pulgadas, podemos calcular el coseno del ángulo a como 6/8 = .750. Si revisamos las tablas trigonométricas o una calculadora elegante, vemos que .750 es el coseno del ángulo 41.41 o . Si no tiene una calculadora elegante y está utilizando las tablas, es posible que deba interpolar. (Pero esa es otra historia).
Dado que el ángulo desconocido = 180- (90 + 41,41) los tres ángulos son 41,41, 90 y 48,59.
Hay otras funciones trigonométricas, pero el seno, el coseno y la tangente harán la mayor parte del trabajo.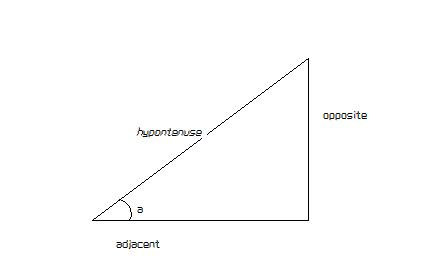
Hay una
Los tres ángulos son
x
2x
2x + 10
Deben sumar 180
x + 2x + 2x + 10 = 180
5x + 10 = 180
5x = 170
x = 34 (ángulo1
2x = 68 (ángulo2)
y = 2x + 10
y = 2 (34) + 10
y = 78 (ángulo3)
34 + 68 + 78 = 180.
Nedra
Todos los ángulos de un triángulo suman 180 grados sin importar el tamaño del triángulo, digamos que 1 ángulo es 50 grados, otro 50 grados y luego ¿cuál es el último 1? Tendría que ser 80 grados --- 50 + 50 + _ = 180? 50 + 50 + 80 = 180.Kadin
Normalmente, en cualquier triángulo, la suma de los tres ángulos es 180. Ya conoces dos ángulos. Tienes que encontrar el ángulo que falta. Considere el triángulo ABC. En este triángulo A, B son los ángulos conocidos. Tenemos que encontrar el ángulo C. la suma de los tres ángulos es 180. entonces, A + B + C = 180, C = 180 - (A + B)Filiberto
Siempre tendrás una longitud de 180 para tu triángulo y cuando sepas que todo fluye desde allí, porque digamos que tus otros dos ángulos son 30 y 20, lo que te da 50, luego restas 50 de 180 y obtienes 130, que será tu falta. ángulo, espero que esto ayude de alguna manera :)Ewald
Hay algunas fórmulas que puedes usar para calcular los grados de un triángulo usando trigonmetría.
A = ángulo 1
b = ángulo 2
c = ángulo 3
A = lado 1
B = lado 2
C = lado 3
a² = b² + c² - 2bc porque A
c² = a² + b² - 2ab porque C
Sin A / a = Sin C / c = Sin B / b
Adyacente significa siguiente o lado a lado. Como ángulos adyacentes o lados adyacentes. La hipotenusa es el lado opuesto del ángulo de 90 grados en un triángulo de ángulo recto. Por ejemplo, si dibuja dos líneas que tienen un ángulo recto, entonces la tercera línea que conecta las dos será hipontenusa.Alec
Sumas los ángulos dados y restas la suma de esos dos números de 180 grados porque no importa lo que el triángulo sume 180 ... Y cualquier respuesta que obtengas es la cantidad de grados que faltan.
Y luego estás listo.
Espero que esto haya ayudado.