Камилла
Вы можете помочь? У меня есть формула, которую я должен использовать: N = -x2-x = 41. Я должен выбрать несколько чисел вместо X, подставить их в формулу и посмотреть, встречаются ли простые числа. Затем я должен попытаться найти число для X, которое, когда я подставляю его, дает
2 Ответы
Клементина
Взгляните на рисунок, чтобы увидеть значение вашей формулы для нескольких различных значений x.
Для x = 0 , N = - (0) 2 - (0) + 41 = -0-0 + 41 = 41 .
Оказывается, 41 - простое число. Вы можете проверить, разделив на нечетные простые числа меньше 7, то есть 3 или 5.
Для x = 1 , N = - (1) 2 - (1) + 41 = -1-1 + 41 = 39 .
39 - составное число, являющееся произведением 3 и 13.
_____
Чтобы проверить число на простоту, вам нужно только разделить на простые числа до квадратного корня из числа. 7 2 = 49, поэтому для всех значений, полученных по этой формуле, потребуется проверка только 3 и 5. Любое четное значение, кроме 2, не является простым. (11, 29, 41 простые числа; 21 = 3 * 7, 35 = 5 * 7, 39 = 3 * 13)
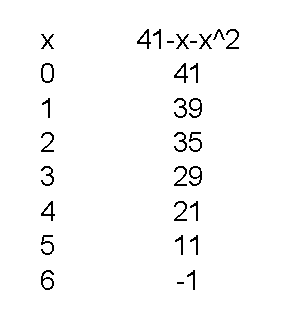
Wilburn
Во-первых, у вас неверная формула. Первый член не является отрицательным, хотя, честно говоря, это не имеет значения, поскольку любое отрицательное число в квадрате положительно. Oddman дал вам некоторую неверную информацию, потому что он использовал уравнение -1-1 + 41 = 39. Поскольку вы не можете возвести в квадрат -1 и получить -1, ваше уравнение фактически будет 1-1 + 41 = 41, поскольку 1-1 = 0 и 0 + 41 = 41. Я использовал эту формулу, заменяя x на несколько четных и нечетных чисел, и до сих пор получал все, кроме простых чисел.