Une particule se déplace le long de l'ellipse 16x2 + 9y2 = 144. Trouvez tous les points (x; y) sur l'ellipse auxquels les taux de changement de x et y par rapport au temps sont égaux. (En supposant que dx=dt et dy=dt ne soient jamais tous les deux nuls au même point.) ?

Si x et y sont des fonctions du temps (t), la dérivée par rapport à t est
  2*16*x*x' + 2*9*y*y' = 0
Si x' = ±y', alors
  ±16x + 9y = 0
  x = ±9y/16 En
branchant ceci dans l'équation de l'ellipse, nous obtenons
  16*(9/16y)^2 + 9*y^2 = 144
  y^2 = 144/(9^2/16+ 9) = 10,24 = 3,2^2
  y = ±3,2
  x = ±9/16*y = ±1,8
Les quatre points où la pente est de ±1 sont (±1,8, ±3,2) .
Si vous insistez pour que les taux de changement soient réellement égaux, plutôt que juste d'une ampleur égale, alors cela ne se produira qu'aux deux points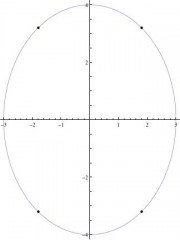
  (x, y) = (-1,8, 3,2) ou (1,8, -3,2),
c'est-à-dire , ces points où la pente est +1.