Abdallah
Trouver les racines de l'équation f(x) = x^3+x-3=0 en utilisant la méthode regula falsi ?
1 Réponses
Imogène
La méthode regula falsi est une méthode itérative de recherche de racine qui utilise une approximation linéaire de la fonction entre des valeurs fonctionnelles de signe opposé connues pour encadrer la racine. Elle est également connue sous le nom de méthode sécante .
La première étape consiste à trouver les valeurs de la variable indépendante pour lesquelles les valeurs de la fonction ont un signe opposé. La règle des signes de Descartes et le théorème de la racine rationnelle peuvent être utiles à cet égard.
Pour votre fonction
f(x) = x^3 + x - 3
Il y a un changement de signe, donc une racine positive. Les racines rationnelles possibles incluent 1 ou 3. En évaluant la fonction pour ces valeurs, nous avons f(1) = -1, f(3) = 27, donc la racine se situe dans l'intervalle ouvert (1, 3). Une vérification que f(2) = 7 peut nous aider à réduire la plage de départ à l'intervalle (1, 2).
L'étape suivante consiste à effectuer l'itération. On peut utiliser comme formule d'itération
x = x1 - (x2 - x1)/(y2 - y1)*y1
où x1 et x2 sont choisis tels que y1=f(x1) et y2=f(x2) aient des signes opposés et un d'entre eux est la valeur la plus récente de x.
On commence par (x1, y1) = (1, -1) et (x2, y2) = (2, 7). Notre prochaine valeur de x sera
x = 1 - (2 - 1)/(7 - (-1))*(-1) = 1 - (1/8)*(-1) = 9/8
Nous trouvons que f(9/8) = -(231/512) < 0, donc notre nouveau (x1, y1) est (9/8, -231/512).
En répétant l'itération, nous trouvons que la convergence est assez lente. Voici les valeurs (x1, x2) pour les 9 premières itérations. On voit que les dernières itérations ont des changements à la 4ème décimale. La valeur de f(x1) à ce stade est de -0,000107134, peut-être assez proche de zéro pour ce que vous voulez.
{1., 2.}, {1.125, 2.}, {1.17798, 2.}, {1.19941, 2.}, {1.20791, 2.},
{1.21126, 2.}, {1.21257, 2.}, {1.21308, 2.}, {1.21328, 2.},
{1.21336, 2.}, {1.21339, 2.}
Mon outil de recherche de racine donne la racine 1.21341.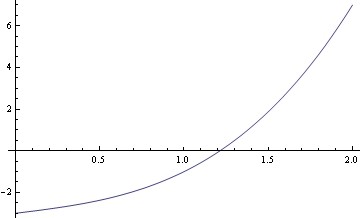
Questions connexes
- Comment puis-je convertir des kilogrammes en pierre ?
- Comment calculer le pourcentage ?
- Comment puis-je calculer les livres (lb) en pierres (st) ?
- Comment calculer le volume d'un cylindre ?
- Comment calculer le pourcentage de pente ?
- Qu'est-ce qu'un polyèdre?
- Comment les nombres arithmétiques ont-ils vu le jour ?
- Qu'est-ce qu'un boulier ?