Joana
Trouver la zone délimitée par l'axe X et la courbe Y=(x-4)(x-2)(x+2) ?
1 Réponses
Hubert
L'aire délimitée sur la région d'intérêt sera l'intégrale définie de cette expression sur la région d'intérêt. L'intégrale de
y = 16 - 4x - 4x^2 + x^3
est
g[x] = Intégrale[y] = 16x - 2x^2 - (4x^3)/3 + x^4/4
Si la région de l'intérêt est x = {-2, 2}, la zone est évaluée à
g[2] - g[-2] = (52/3 - (-76/3)) = 128/3.
S'il vous plaît jeter un oeil à l'image.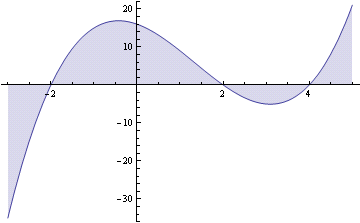
Questions connexes
- Comment puis-je convertir des kilogrammes en pierre ?
- Comment calculer le pourcentage ?
- Comment puis-je calculer les livres (lb) en pierres (st) ?
- Comment calculer le volume d'un cylindre ?
- Comment calculer le pourcentage de pente ?
- Qu'est-ce qu'un polyèdre?
- Comment les nombres arithmétiques ont-ils vu le jour ?
- Qu'est-ce qu'un boulier ?