sin(15 degré+x)+sin(45 degré-x)=1 Qu'est-ce que x est égal ?

Péché (15°+x) + Péché(45°-x) = 1

Pour commencer à résoudre ce problème, vous devez utiliser la formule somme-produit* pour l'addition de deux termes sinus, où sin(a) + sin(b) = 2sin[(a+b)/2]cos[(ab )/2]. Dans ce cas, la valeur pour "a" est 15°+x et la valeur pour "b" est 45°-x. Alors ajoutons ces valeurs, d'accord ?

2sin[(15°+x)+(45°-x) /2]cos[(15°+x)-(45°-x) /2] = 1

Simplifiez les termes entre parenthèses pour les valeurs sinus et cosinus. Dans (15°+x)+(45°-x), puisqu'on les additionne, on peut directement additionner 15 avec 45 pour donner 60 degrés. Et quand nous ajoutons x avec moins x, cela s'annule simplement à 0, donc 60 + 0 est toujours 60. Et nous divisons également toute cette somme par 2, donc 60 divisé par 2 est égal à 30 degrés.

2sin(30°)cos[(15°+x)-(45°-x) /2] = 1

Pour (15°+x)-(45°-x), notez qu'il y a une soustraction en cours. Nous allons distribuer cela à 45 degrés et -x, comme ceci :

2sin(30°)cos(15°+x-45°+x /2) = 1

Remarquez comment le 45° était à l'origine positif, mais est devenu négatif puisque nous lui avons distribué un signe négatif ainsi qu'au -x. Lorsque vous ajoutez un négatif à quelque chose qui est déjà négatif, il devient positif, donc -x devient un x positif. Maintenant, combinons-les.

15° moins 45° se transforme en -30°, et x+x se transforme en 2x, nous avons donc 2x - 30°. Mais nous divisons également toute cette différence par 2, donc (2x-30°)/2 = x-15°. Maintenant nous avons:

2sin(30°)cos(x-15°) = 1

Oh regarde, nous avons sin(30°) dans l'équation. Cool, regardons quelle est sa valeur sur le cercle unité.

Maintenant que nous savons que sin(30) est 1/2, revenons à notre équation.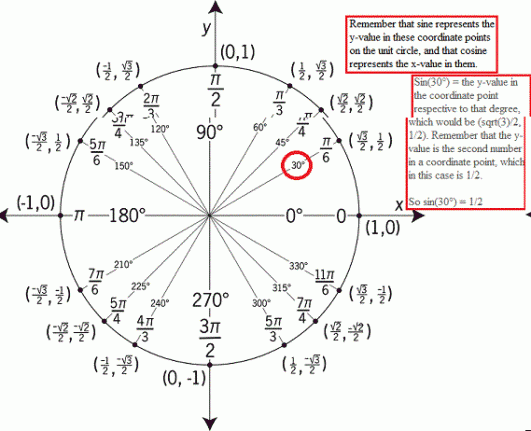

2sin(30°)cos(x-15°) = 1

Si nous branchons 1/2 pour sin(30), nous devons également le multiplier par 2, donc 1/2 * 2 est égal à 1. Et 1 fois cos(x-15) est juste cos(x-15) , on aura donc :

cos(x-15) = 1

Maintenant, réfléchissez à ceci, quel degré le cosinus doit-il avoir pour être exactement égal à 1 ? N'oubliez pas que sur un cercle unité, l'axe horizontal représente les valeurs de x. Le cercle s'étend jusqu'aux valeurs x -1 et 1 de gauche à droite, ainsi qu'aux valeurs y -1 à 1 de bas en haut. Étant donné que le cosinus se concentre sur les valeurs x, faites attention à l'axe horizontal. Où serait le cosinus de quelque chose d'égal à 1 ?

Réponse : Le cosinus de quelque chose est égal à 1 lorsque ce quelque chose est à 0 degré, ou 360n degrés. Vous voyez, lorsque nous avons cos(0), le point de coordonnée correspondant à 0 degré est (1,0), et puisque nous savons que le cosinus se concentre sur les valeurs x, notre réponse à cos(0) sera 1. Donc cos (0) = 1.

Bien sûr, vous pouvez toujours y ajouter 360, car cela vous donnera la même réponse. Le cercle de l'unité s'étend à 360 degrés, donc faire le tour du cercle entier une fois vous ramènera à l'endroit où vous avez commencé. Donc d'autres choix valides pourraient être cos(360), cos(720), cos(1080), etc. ).

Bon, revenons à notre équation. On a:

cos(x-15) = 1

Alors, quelle valeur doit avoir x pour obtenir cos(0), puisque nous savons maintenant que cos(0) = 1 ? Eh bien, c'est facile, il suffit de définir x - 15 égal à 0 et de résoudre x.

x - 15 = 0

x = 15 (ajouté 15 des deux côtés)

Donc x est égal à 15 degrés. Mais rappelez-vous, vous pouvez également y ajouter n'importe quelle quantité de 360, car cela vous donnera la même réponse, car l'ajout de 360 ​​degrés signifie que vous ferez le tour du cercle de l'unité une fois et reviendrez là où vous avez commencé. Donc la vraie réponse ici est

x = 15° + 360°n