Quelles sont les trois techniques permettant de résoudre une équation quadratique ? Démontrez les trois techniques à l'aide de l'équation « 9x2 + 3x - 6 = 0. »

1.) Équation quadratique

2.) Compléter le carré

3.) Facteur par regroupement

Méthode 1 - L'équation quadratique est :

Pour factoriser à l'aide de cette formule, vous devez insérer des valeurs numériques pour les trois variables de la formule : A, b et c. La valeur numérique pour "a" est le nombre associé à la variable "x^2". La valeur numérique pour "b" est le nombre associé à la variable "x". Et la valeur numérique pour "c" est le nombre constant auquel aucune variable n'est attachée.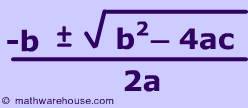

Dans l'équation que vous avez donnée, 9x^2 + 3x - 6 = 0, 9 représente a, 3 représente b et -6 représente c. Insérez simplement ces trois nombres dans l'équation, simplifiez et vous obtiendrez vos solutions x.

Méthode 2 - Compléter le carré

9x^2 + 3x = 6 (Ajouter 6 des deux côtés)

x^2 + (x/3) = (2/3) (Diviser les deux côtés par 9)

x^2 + 2(x/6) = (2/3)

x^2 + 2(x/6) + (1/6)^2 = (2/3) + (1/6)^2 [Ajouter (1/6)^2 des deux côtés]

(x + 1/6)^2 = 2/3 + 1/36 (Simplifier)

(x + 1/6)^2 = 24/36 + 1/36

(x + 1/6)^2 = 25/36

Prenez la racine carrée des deux côtés.

carré[(x + 1/6)^2] = carré (25/36)

x + 1/6 = 5/6 (Simplifier)

x = 4/6 = 2/3 (Simplifier davantage)

Méthode 3 - Facteur par regroupement

Tout d'abord, multipliez les valeurs de a et c ensemble. Dans 9x^2 + 3x - 6 = 0, a = 9 et c = -6, donc les multiplier ensemble donnera -54.

Maintenant, pensez à quels facteurs de ce nombre, -54, s'additionneront à la valeur de b, qui est 3 ? (Prendre la somme signifie additionner). Les facteurs sont 9 et -6, car si vous les additionnez, vous obtiendrez 3.

Considérez 3x comme 9x/5 et 6x/5 (car l'addition de ces deux fractions vous donnera 3x). On peut donc réécrire l'équation sous la forme :

9x^2 + 9x/5 + 6x/5 - 6

Regroupez maintenant les deux paires et retirez-en les termes communs. Observer:

(9x^2 + 9x/5) + (6x/5 - 6)

= 9x(x + 1/5) + 6(x/5 - 1)

= 9x(x + 1/5) + 1,2(x + 1/5)

Vous pouvez voir qu'il y a deux de (x + 1/5), avec des nombres constants différents se produisant avant. Lorsque vous rencontrez cela, vous devez supprimer les facteurs communs et réécrire sous forme de facteurs groupés :

(9x + 1,2)(x + 1/5)

Dans l'ensemble, la méthode 1 est de loin la méthode la plus simple à faire. Vous avez juste besoin de mémoriser une formule et de saisir des nombres, plutôt que de faire tout ce travail pour les autres méthodes.