Pouvez-vous trouver les points de discontinuité, le cas échéant A) F(x)=(1/(1-2sinx)) B) F(x)=(3/(5+2cosx)) ?

Les points de discontinuité se produisent là où le dénominateur passe à zéro et change de signe.

A) 1-2sin[x] = 0
  1 = 2sin[x]
  1/2 = sin[x].
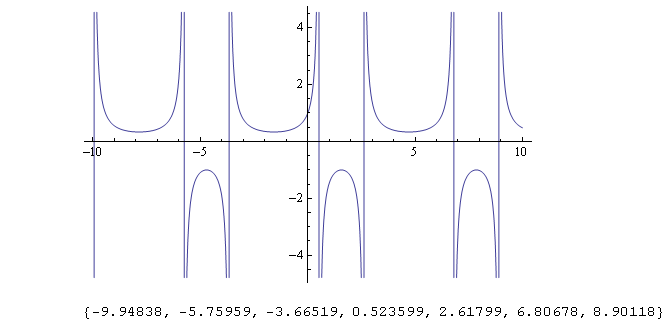
  Cela se produira à x=(4n+1)Pi/2±Pi/3 radians = (4n+1)90±60 degrés, où n est un nombre entier. Regarder la photo.

B) Il n'y a pas de points de discontinuité, car la magnitude minimale que le dénominateur peut avoir est de 3. Il ne va jamais à zéro.