Pouvez-vous indiquer le nombre possible de zéros imaginaires de F(x) = 10x3 - 4x2 + 2x - 6 ?

Étant donné une équation cubique de la forme ax ³ +bx ² +cx+d=0, une formule agaçante compliquée pour le "discriminant" vous dira combien de racines réelles l'équation a. Le discriminant est 18abcd-4(ac ³ +b ³ d)+b ² c ² -27a ² d ² . S'il est <0, il y a deux racines complexes et une vraie racine. Si c'est =0, toutes les racines sont réelles et au moins deux d'entre elles sont égales. Si le discriminant est > 0, il y a trois racines réelles inégales.

Un autre test rapide, mais pas si complet, consiste à regarder b ²-3ac. Si cette valeur est <0, l'équation n'a qu'une seule racine réelle. Si cette valeur est =0 ou >0, on peut dire quelque chose sur le nombre de points d'inflexion dans le graphique de ax ³ +bx ² +cx+d, mais c'est tout.

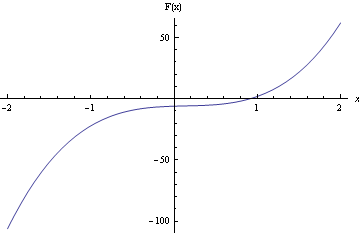
Ainsi, dans votre F(x) = 10x ³ - 4x ² + 2x - 6, la valeur de b ² -3ac est (-4) ² -3(10)(2)=16-60=-44. Ainsi, la fonction F(x) est monotone (n'a pas de points d'inflexion) et il n'y a qu'une seule racine réelle. Les deux autres racines doivent être complexes, c'est-à-dire qu'elles ont une partie imaginaire non nulle.