Ellis
Initialement, 50 livres de sels sont dissous dans un grand réservoir contenant 300 gallons d'eau. Une solution de saumure est pompée dans le réservoir à un débit de 3 gal/min et une solution bien agitée est ensuite pompée au même débit ?
1 Réponses
Emelia
Supposons que la quantité totale de sels dans le réservoir soit de s[t] livres, où t est le temps en minutes. On nous dit que
s[0] = 50 livres
Le taux d'augmentation de s[t] est
(3 gal/min)*(2 lb/gal) = 6 lb/min
Le taux de diminution de s[t] (en livres par minute) est
s/(300 gal)*(3 gal/min) En
exprimant ces relations à l'aide d'une équation différentielle, on a
s'[t] = 6 - (1/100)*s,
s[0] = 50
Nous reconnaissons que la solution de cette équation linéaire non homogène à coefficients constants sera de la forme
s[t] = c 1 e^(a*t) + c 0 pour certaines valeurs de a et constantes c n .
En substituant cela dans l'équation différentielle ci-dessus et en faisant correspondre les coefficients, nous obtenons
c 1 *a*e^(a*t) = 6 - (1/100)*c 1 *e^(a^t) - (1/100) )*c 0 c 1 *a = -(1/100)*c 1 (coefficients de correspondance de e^(a*t))
a = -1/100 0 = 6 - (1/100)*c 0 (correspondance constantes)
c 0 = 600 c 1 *e^(-0/100) + 600 = 50 (évaluer pour la condition initiale)
c 1 = 50 - 600 = -550La quantité de sel est
s[t] = 600 - 550e^(-t/100)) Après 50 minutes, la quantité de sel dans le réservoir sera
s[50] = 600 - 550*e^(-1/2)
s [50] ≈ 266,4 livres de sels La quantité présente lorsque t devient très grand sera
s[infini] = 600 livres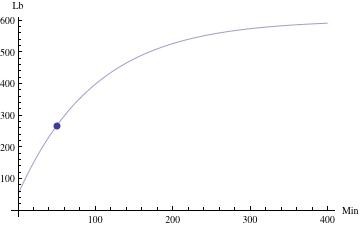
Questions connexes
- Comment puis-je convertir des kilogrammes en pierre ?
- Comment calculer le pourcentage ?
- Comment puis-je calculer les livres (lb) en pierres (st) ?
- Comment calculer le volume d'un cylindre ?
- Comment calculer le pourcentage de pente ?
- Qu'est-ce qu'un polyèdre?
- Comment les nombres arithmétiques ont-ils vu le jour ?
- Qu'est-ce qu'un boulier ?