Si dos vértices de un triángulo equilátero son (-4, -3) y (4, 1), ¿encuentra el vértice restante?

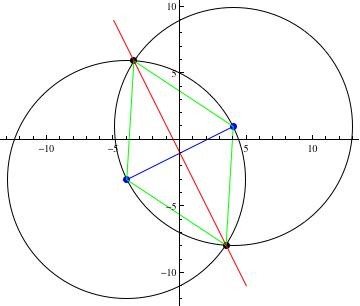
Habrá dos de esos vértices. Uno estará en el segundo cuadrante y el otro estará en el cuarto cuadrante. Se ubicarán en la bisectriz perpendicular de la línea entre los puntos dados, y se encontrarán en los puntos de intersección de círculos centrados en cada punto que tienen un radio igual a la distancia entre los puntos. (Consulte la figura siguiente.)

La distancia entre los puntos dados es
  r = √ ((- 4-4) ^ 2 + (-3-1) ^ 2) = √ (64 + 16) = √80

El círculo centrado en (-4, -3) tiene la ecuación
  (x + 4) ^ 2 + (y + 3) ^ 2 = 80
  x ^ 2 + 8x + 16 + y ^ 2 + 6y + 9 = 80 (expansión de la ecuación. Llame a esto [1])

El círculo centrado en (4, 1) tiene la ecuación
  (x - 4) ^ 2 + (y - 1) ^ 2 = 80
  x ^ 2 - 8x + 16 + y ^ 2 - 2y + 1 = 80 (expansión de la ecuación. Llame a esto [2])

Podemos establecer [1] = [2] y resolver para y.
  x ^ 2 + 8x + 16 + y ^ 2 + 6y + 9 = 80 = x ^ 2 - 8x + 16 + y ^ 2 - 2y + 1
  8x + 6y + 9 = -8x - 2y + 1 (restar x ^ 2 + 16 + y ^ 2 de ambos lados)
  6y = -16x - 2y - 8 (restar 8x + 9 de ambos lados)
  8y = -16x - 8 (sumar 2y)
  y = -2x - 1 (dividir entre 8. Esto es la ecuación de la línea roja. Llame a esto [3])

Podemos sustituir [3] en [1] y resolver para x. En la figura, esto da la coordenada x de los puntos de intersección de la línea roja y el círculo inferior.
  x ^ 2 + 8x + 16 + ( -2x - 1 ) ^ 2 + 6 ( -2x - 1 ) + 9 = 80
  x ^ 2 + 8x + 16 + 4x ^ 2 + 4x + 1 - 12x - 6 + 9 = 80 (eliminar paréntesis)
  5x ^ 2 + 20 = 80 (recopilar términos)
  5x ^ 2 = 60 (restar 20)
  x ^ 2 = 12 (dividir por 5)
  x = ± 2√3     (sacar la raíz cuadrada)

Podemos usar este resultado en [3] para encontrar los valores correspondientes de y. (Primero el signo positivo).
  Y = -2 (2√3) - 1 = -4√ (3) - 1
El vértice del cuadrante IV es (2√3, -4√ (3) - 1) .

  y = -2 (-2√3) - 1 = 4√ (3) - 1
El vértice del cuadrante II es (-2√3, 4√ (3) - 1) .