Welche trigonometrischen Grundfunktionen haben vertikale Asymptoten?

Denken Sie daran, dass vertikale Asymptoten auftreten, wenn der Nenner einer Funktion gleich Null ist.

Durch Grundtrigger. Funktionen, ich nehme an du meinst sin/cos/tan.

Siehe diesen Einheitskreis. Wenn Sie einen Sinus eines bestimmten Grades haben, messen Sie den y-Wert in diesem Grad. Wenn Sie also f(x) = sin(90) haben, achten Sie genau darauf, wo 90 Grad auf dem Einheitskreis sind. Ganz oben, oder? Und da der Sinus den y-Wert bei diesem Grad misst, können wir sagen, dass der Wert bei 90 Grad 1 ist. Also sin(90) = 1.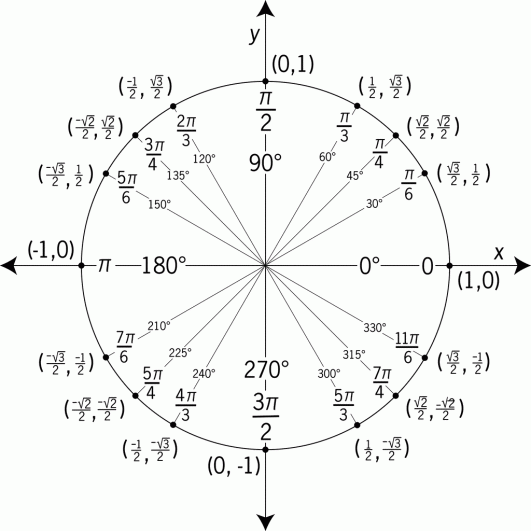

Kosinus eines bestimmten Grades misst den x-Wert bei diesem Grad. Nehmen wir an, wir haben f(x) = cos(60). Schauen Sie sich den Einheitskreis an, bei dem sich 60 Grad befinden, und messen Sie den x-Wert an diesem Punkt. Es wäre 1/2, also können wir sagen, dass cos(60) = 1/2 ist.

Tangente eines bestimmten Grades misst den y-Wert geteilt durch den x-Wert bei diesem Grad. Wenn f(x) tan(60) wäre, würden Sie sich den Teil des Einheitskreises ansehen, in dem 60 Grad angegeben ist, und den y-Wert durch den x-Wert teilen, und das wäre die Antwort für tan (60). In diesem Fall gilt tan(60) = [sqrt(3)/2]/(1/2) = sqrt(3)/1 = sqrt(3), was ungefähr 1,73 entspricht.

Kommen wir nun zu Ihrer Frage zu vertikalen Asymptoten zurück. Wie gesagt, der Nenner muss Null sein und der Zähler kann eine beliebige Zahl sein.

f(x) = tanx = sinx/cosx

Wenn wir 90 Grad für x einstecken, erhalten wir:

f(90) = tan(90) = sin(90)/cos(90) = 1/0

Der Grund dafür, dass der Nenner Null ist, liegt darin, dass der bei 90 Grad gemessene Kosinus Null als Wert hat.

Aber warte eine Sekunde...

f(270) = tan(270) = sin(270)/cos(270) = -1/0

Es gibt mehr als einen Wert, der dazu führen kann, dass eine grundlegende trigonometrische Funktion einen Nenner von Null hat. Und es ist nicht nur Kosinus. Sinus und Tangens können bei 0 Grad und 180 Grad Null sein.

Jede grundlegende trigonometrische Funktion kann also vertikale Asymptoten haben. Es muss nur im Nenner stehen und gleich Null sein.