Welche drei Techniken können verwendet werden, um eine quadratische Gleichung zu lösen? Zeigen Sie alle drei Techniken mit der Gleichung "9x2 + 3x - 6 = 0".

1.) Quadratische Gleichung

2.) Quadrat vervollständigen

3.) Faktor durch Gruppierung

Methode 1 - Die quadratische Gleichung lautet:

Um mit dieser Formel zu faktorisieren, müssen Sie numerische Werte für alle drei Variablen in der Formel einsetzen: A, b und c. Der numerische Wert für "a" ist die Zahl, die der Variablen "x^2" zugeordnet ist. Der numerische Wert für "b" ist die Zahl, die der Variablen "x" zugeordnet ist. Und der numerische Wert für "c" ist die konstante Zahl, an die keine Variable angehängt ist.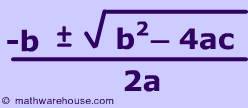

In der von Ihnen angegebenen Gleichung ist 9x^2 + 3x - 6 = 0, 9 steht für a, 3 steht für b und -6 steht für c. Setze einfach diese drei Zahlen in die Gleichung ein, vereinfache und du erhältst deine x-Lösungen.

Methode 2 - Das Quadrat vervollständigen

9x^2 + 3x = 6 (Addiere 6 zu beiden Seiten)

x^2 + (x/3) = (2/3) (Beide Seiten durch 9 teilen)

x^2 + 2(x/6) = (2/3)

x^2 + 2(x/6) + (1/6)^2 = (2/3) + (1/6)^2 [Zu beiden Seiten (1/6)^2 hinzufügen]

(x + 1/6)^2 = 2/3 + 1/36 (vereinfachen)

(x + 1/6)^2 = 24/36 + 1/36

(x + 1/6)^2 = 25/36

Ziehe die Quadratwurzel von beiden Seiten.

Quadrat[(x + 1/6)^2] = Quadrat(25/36)

x + 1/6 = 5/6 (vereinfachen)

x = 4/6 = 2/3 (weiter vereinfachen)

Methode 3 - Faktor durch Gruppierung

Multiplizieren Sie zunächst die Werte von a und c miteinander. In 9x^2 + 3x - 6 = 0, a = 9 und c = -6, also multipliziert man sie miteinander, ergibt -54.

Überlegen Sie nun, welche Faktoren dieser Zahl, -54, den Wert von b ergeben, der 3 ist? (Die Summe zu nehmen bedeutet zu addieren). Die Faktoren sind 9 und -6, denn wenn Sie sie addieren, erhalten Sie 3.

Stellen Sie sich 3x als 9x/5 und 6x/5 vor (da die Addition dieser beiden Brüche 3x ergibt). Wir können die Gleichung also umschreiben als:

9x^2 + 9x/5 + 6x/5 - 6

Gruppieren Sie nun die beiden Paare und nehmen Sie dort gemeinsame Begriffe heraus. Beobachten:

(9x^2 + 9x/5) + (6x/5 - 6)

= 9x(x + 1/5) + 6(x/5 - 1)

= 9x(x + 1/5) + 1,2(x + 1/5)

Sie können sehen, dass es dort zwei von (x + 1/5) gibt, mit unterschiedlichen konstanten Zahlen davor. Wenn Sie darauf stoßen, müssen Sie die gemeinsamen Faktoren entfernen und als gruppierte Faktoren neu schreiben:

(9x + 1,2)(x + 1/5)

Insgesamt ist Methode 1 bei weitem die einfachste Methode. Sie müssen sich nur eine Formel merken und Zahlen eingeben, anstatt all diese Arbeit für die anderen Methoden zu erledigen.