sin(15 Grad+x)+sin(45 Grad-x)=1 Was ist x gleich?

Sin(15°+x) + Sin(45°-x) = 1

Um dieses Problem zu lösen, müssen Sie die Summe-zu-Produkt-Formel* für die Addition von zwei Sinustermen verwenden, wobei sin(a) + sin(b) = 2sin[(a+b)/2]cos[(ab )/2]. In diesem Fall beträgt der Wert für "a" 15°+x und der Wert für "b" beträgt 45°-x. Setzen wir also diese Werte ein, oder?

2sin[(15°+x)+(45°-x) /2]cos[(15°+x)-(45°-x) /2] = 1

Vereinfachen Sie die Terme innerhalb der Klammern für Sinus- und Kosinuswerte. In (15°+x)+(45°-x) können wir, da wir sie addieren, direkt 15 mit 45 addieren, um 60 Grad zu erhalten. Und wenn wir x mit negativem x addieren, hebt das einfach auf 0 auf, also ist 60 + 0 immer noch 60. Und wir teilen auch diese gesamte Summe durch 2, also ist 60 geteilt durch 2 gleich 30 Grad.

2sin(30°)cos[(15°+x)-(45°-x) /2] = 1

Beachten Sie, dass für (15°+x)-(45°-x) eine gewisse Subtraktion stattfindet. Wir werden das auf 45 Grad und -x verteilen, wie folgt:

2sin(30°)cos(15°+x-45°+x /2) = 1

Beachten Sie, dass der 45° ursprünglich positiv war, aber negativ wurde, da wir sowohl auf ihn als auch auf das -x negative Vorzeichen verteilt haben. Wenn Sie etwas Negatives zu etwas hinzufügen, das bereits negativ ist, wird es positiv, also wird aus -x ein positives x. Jetzt kombinieren wir sie.

15° minus 45° wird zu -30° und x+x wird zu 2x, also haben wir 2x - 30°. Aber wir teilen auch diese gesamte Differenz durch 2, also (2x-30°)/2 = x-15°. Jetzt haben wir:

2sin(30°)cos(x-15°) = 1

Oh schau, wir haben Sünde (30°) in der Gleichung. Cool, schauen wir uns an, was der Wert davon auf dem Einheitskreis ist.

Da wir nun wissen, dass sin(30) 1/2 ist, schauen wir uns unsere Gleichung noch einmal an.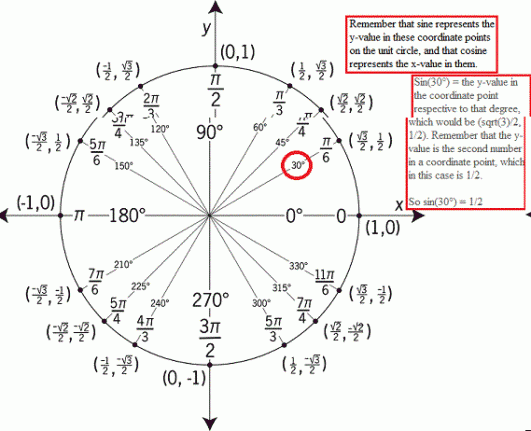

2sin(30°)cos(x-15°) = 1

Wenn wir 1/2 für sin(30) einsetzen, müssen wir es auch mit 2 multiplizieren, also ist 1/2 * 2 gleich 1. Und 1 mal cos(x-15) ist nur cos(x-15) , also haben wir:

cos(x-15) = 1

Denken Sie jetzt darüber nach, welchen Grad muss der Kosinus genau gleich 1 sein? Denken Sie daran, dass auf einem Einheitskreis die horizontale Achse Werte für x darstellt. Der Kreis erstreckt sich von links nach rechts auf die x-Werte -1 und 1 sowie von unten nach oben auf die y-Werte -1 bis 1. Da sich der Kosinus auf x-Werte konzentriert, achten Sie auf die horizontale Achse. Wo wäre der Kosinus von etwas gleich 1?

Antwort: Der Kosinus von etwas ist gleich 1, wenn dieses etwas bei 0 Grad oder 360n Grad ist. Sie sehen, wenn wir cos(0) haben, ist der Koordinatenpunkt, der 0 Grad entspricht, (1,0), und da wir wissen, dass sich der Kosinus auf x-Werte konzentriert, ist unsere Antwort auf cos(0) 1. Also cos (0) = 1.

Natürlich können Sie immer nur 360 hinzufügen, da Sie die gleiche Antwort erhalten. Der Einheitskreis dehnt sich auf volle 360 ​​Grad aus. Wenn Sie also einmal den ganzen Kreis umrunden, gelangen Sie zurück zu Ihrem Ausgangspunkt. Andere gültige Optionen könnten also cos(360), cos(720), cos(1080) usw. sein. (Hier kommt 360n ins Spiel. Das "n" gibt an, wie oft Sie 360 ​​hinzufügen, also muss es eine ganze Zahl sein ).

In Ordnung, also schauen wir uns unsere Gleichung noch einmal an. Wir haben:

cos(x-15) = 1

Welchen Wert muss x haben, um cos(0) zu erhalten, da wir jetzt wissen, dass cos(0) = 1 ist? Nun, es ist einfach, setze einfach x - 15 gleich 0 und löse nach x auf.

x - 15 = 0

x = 15 (auf beiden Seiten 15 hinzugefügt)

Also ist x gleich 15 Grad. Aber denken Sie daran, Sie können auch einen beliebigen Betrag von 360 hinzufügen, da Sie die gleiche Antwort erhalten, da das Hinzufügen von 360 Grad bedeutet, dass Sie den gesamten Einheitskreis einmal umrunden und wieder dort landen, wo Sie begonnen haben. Die wahre Antwort hier ist also

x = 15° + 360°n