Pattie
Ok, ich brauche Hilfe bei der Mathe der Henkersabteilung. Niemand scheint eine Antwort zu haben. HILFE?
1 Antworten
Amir
Es ist schwer, eine Antwort zu geben, wenn es keine Frage gibt.
Hier ist eine PowerPoint-Datei , die die Methode Schritt für Schritt zeigt. Der Name der Methode scheint sich von der besonderen Form der Klammer abzuleiten, die verwendet wird, um den Quotienten und seine Arithmetik von der mit dem Dividenden verbundenen Berechnung und Subtraktion zu trennen.
Die in der Datei gezeigte Methode lässt Sie die höchste Quotientenziffer erraten, dann multiplizieren und subtrahieren Sie auf die übliche Weise für die lange Division. Wenn Sie etwas niedrig geraten haben, ist das in Ordnung, denn am Ende addieren Sie einfach die partiellen Quotientenwerte.
Unten haben Sie einen Rest. Diese Methode eignet sich beispielsweise nicht gut zur Bestimmung von Dezimaläquivalenten von Brüchen, es sei denn, Sie erweitern den Dividenden nach rechts, bevor Sie beginnen.
Die folgende Grafik zeigt 1 abgeschlossenes "guess" und ein zweites "guess" beim Quotienten mit in Arbeit befindlichen Arbeiten. Jeder geschätzte Quotient wird mit dem Divisor multipliziert und vom aktuellen Dividenden abgezogen, um einen neuen Dividenden zu erhalten. Quotientenschätzungen werden rechts vom vertikalen Balken notiert.
Am Ende, wenn der verbleibende Dividenden kleiner als der Divisor ist, addieren Sie die Quotientenschätzungen, um die endgültige Quotientenantwort zu erhalten. Der verbleibende Dividendenwert ist der Rest der Divisionsoperation.
Der nächste Schritt in der gezeigten Aufgabe besteht darin, 80 von 97 zu subtrahieren, um 17 zu erhalten. Schätzen Sie nun, wie oft 8 in 17 eingeht. Es wird 2 sein, also schreiben wir 2 rechts von der vertikalen Linie, und berechne 2*8 = 16. Subtrahieren von 16 erhalten wir den Rest von 1. Addiert man die partiellen Quotienten rechts, erhält man 10+10+2 = 22. Wir haben 177/8 = 22 Rest 1 berechnet.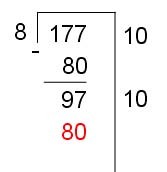
Verwandte Fragen
- Wie können wir Zwölftausend Zwölfhundert und Zwölf in Ziffern schreiben?
- Können Sie zeigen, dass die Summe einer irrationalen und einer rationalen Zahl immer eine irrationale Zahl ist?
- Was bedeutet Viereck?
- Was bedeutet Quotient?
- Wie finden Sie die Fläche eines Achtecks?
- Wie finde ich die Höhe eines Trapezes? Eine Basis ist 10, die andere Basis ist unbekannt und die beiden anderen Seiten sind 15 und 13.
- Wie heißt ein zehnseitiges Objekt?
- Was bedeutet symmetrisch?