Ist eine horizontale Parabel eine Funktion?

Ja, es ist eine Funktion.

Sie stimmen zu, dass y = x^2 Ihnen ein "U"-förmiges Diagramm liefert, oder? Und y = -x^2 dreht diese "U"-Kurve auf den Kopf. In beiden Parabeln zeigen sie vertikal.

Aber diese Parabeln können auch horizontal zeigen. Anstatt "x" die quadrierte Variable zu sein, wird es diesmal "y" sein.

x = y^2 gibt Ihnen eine horizontale Parabel, und um dies zu beweisen, wenn Sie nach y auflösen würden (was plus oder minus Quadratwurzel von x ergeben würde), ist die Kurve von y = sqrt(x) genau die gleiche eins als x = y^2.

Diagramm für y = sqrt(x):

Diagramm für x = y^2: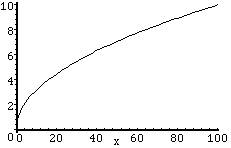

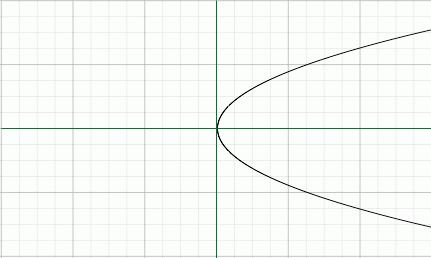
Der einzige Unterschied zwischen x = y^2 und y = sqrt(x) besteht darin, dass die Kurve für x = y^2 für die untere Hälfte des Graphen funktioniert, im Vergleich zur Kurve von y = sqrt(x), die dies tut nicht.

Nicht sicher.

Es besteht den vertikalen Linientest nicht, aber meine Erinnerung an diese besondere Situation ist verschwommen.

Vielleicht wird David das sehen und antworten.