Abdullah
Finden Sie die Wurzeln der Gleichung f(x) = x^3+x-3=0 mit der Regula-Falsi-Methode?
1 Antworten
Imogene
Das Regula-Falsi- Verfahren ist ein iteratives Verfahren zur Wurzelfindung, das eine lineare Approximation der Funktion zwischen funktionalen Werten mit entgegengesetztem Vorzeichen verwendet, von denen bekannt ist, dass sie die Wurzel einklammern. Sie wird auch als Sekantenmethode bezeichnet .
Der erste Schritt besteht darin, Werte der unabhängigen Variablen zu finden, für die die Werte der Funktion entgegengesetzte Vorzeichen haben. Dabei können die Descartes-Zeichenregel und der Rational-Wurzel-Satz hilfreich sein.
Für Ihre Funktion
f(x) = x^3 + x - 3
Es gibt einen Vorzeichenwechsel, also eine positive Wurzel. Mögliche rationale Wurzeln sind 1 oder 3. Wenn wir die Funktion für diese Werte auswerten, haben wir f(1) = -1, f(3) = 27, also liegt die Wurzel im offenen Intervall (1, 3). Eine Überprüfung, dass f(2) = 7 ist, kann uns helfen, den Startbereich auf das Intervall (1, 2) einzugrenzen.
Der nächste Schritt besteht darin, die Iteration durchzuführen. Als Iterationsformel können wir
x = x1 - (x2 - x1)/(y2 - y1)*y1 verwenden,
wobei x1 und x2 so gewählt werden, dass y1=f(x1) und y2=f(x2) entgegengesetzte Vorzeichen haben und eins von ihnen ist der neueste Wert von x.
Wir beginnen mit (x1, y1) = (1, -1) und (x2, y2) = (2, 7). Unser nächster Wert von x ist
x = 1 - (2 - 1)/(7 - (-1))*(-1) = 1 - (1/8)*(-1) = 9/8
Wir finden, dass f(9/8) = -(231/512) < 0 ist, also ist unser neues (x1, y1) (9/8, -231/512).
Wenn wir die Iteration wiederholen, stellen wir fest, dass die Konvergenz ziemlich langsam ist. Hier sind die (x1, x2) Werte für die ersten 9 Iterationen. Wir sehen, dass die letzten Iterationen Änderungen an der 4. Dezimalstelle aufweisen. Der Wert von f(x1) ist an diesem Punkt -0,000107134, vielleicht nahe genug an Null für das, was Sie wollen.
{1., 2.}, {1.125, 2.}, {1.17798, 2.}, {1.19941, 2.}, {1.20791, 2.},
{1.21126, 2.}, {1.21257, 2.}, {1.21308, 2.}, {1.21328, 2.},
{1.21336, 2.}, {1.21339, 2.}
Mein Root-Finder gibt die Root als 1.21341 an.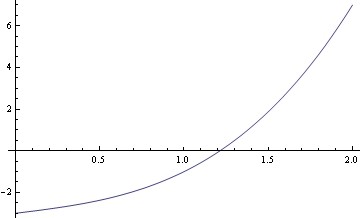
Verwandte Fragen
- Wie können wir Zwölftausend Zwölfhundert und Zwölf in Ziffern schreiben?
- Können Sie zeigen, dass die Summe einer irrationalen und einer rationalen Zahl immer eine irrationale Zahl ist?
- Was bedeutet Viereck?
- Was bedeutet Quotient?
- Wie finden Sie die Fläche eines Achtecks?
- Wie heißt ein zehnseitiges Objekt?
- Was bedeutet symmetrisch?
- Was ist eine "skalare" Größe? Bitte geben Sie Beispiele.