Ein Teilchen bewegt sich entlang der Ellipse 16x2 + 9y2 = 144. Finden Sie alle Punkte (x; y) auf der Ellipse, an denen die zeitlichen Änderungsraten von x und y gleich sind. (Angenommen, dx=dt und dy=dt sind niemals beide gleichzeitig Null.)?

Wenn x und y Funktionen der Zeit (t) sind, ist die Ableitung nach t
  2*16*x*x' + 2*9*y*y' = 0
Wenn x' = ±y', dann
  ±16x + 9y = 0
  x = ±9y/16 Setzen
wir dies in die Gleichung für die Ellipse ein, erhalten wir
  16*(9/16y)^2 + 9*y^2 = 144
  y^2 = 144/(9^2/16+ 9) = 10,24 = 3,2^2
  y = ±3,2
  x = ±9/16*y = ±1,8
Die vier Punkte, an denen die Steigung ±1 beträgt, sind (±1,8, ±3,2) .
Wenn Sie darauf bestehen, dass die Änderungsraten tatsächlich gleich und nicht nur gleich groß sind, dann geschieht dies nur an den beiden Punkten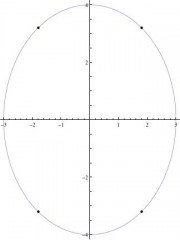
  (x, y) = (-1.8, 3.2) oder (1.8, -3.2),
also , die Punkte, an denen die Steigung +1 beträgt.