Ellis
Anfänglich werden 50 Pfund Salze in einem großen Tank mit 300 Gallonen Wasser gelöst. Eine Solelösung wird mit einer Geschwindigkeit von 3 gal/min in den Tank gepumpt und eine gut gerührte Lösung wird dann mit derselben Geschwindigkeit abgepumpt?
1 Antworten
Emelia
Angenommen, die Gesamtmenge an Salzen im Tank beträgt s[t] Pfund, wobei t die Zeit in Minuten ist. Uns wird gesagt, dass
s[0] = 50 Pfund
Die Zunahmerate von s[t] beträgt
(3 gal/min)*(2 lb/gal) = 6 lb/min
Die Abnahmerate von s[t] (in Pfund pro Minute) ist
s/(300 gal)*(3 gal/min)
Wenn wir diese Beziehungen mit einer Differentialgleichung ausdrücken, haben wir
s'[t] = 6 - (1/100)*s,
s[0] = 50
Wir erkennen, dass die Lösung dieser linearen inhomogenen Gleichung mit konstanten Koeffizienten die Form
s[t] = c 1 e^(a*t) + c 0 . hat für einige Werte von a und Konstanten c n .
Wenn wir dies in die obige Differentialgleichung einsetzen und die Koeffizienten anpassen, erhalten wir
c 1 *a*e^(a*t) = 6 - (1/100)*c 1 *e^(a^t) - (1/100 )*c 0 c 1 *a = -(1/100)*c 1 (
Matchkoeffizienten von e^(a*t)) a = -1/100 0 = 6 - (1/100)*c 0 (Match Konstanten)
c 0 = 600 c 1 *e^(-0/100) + 600 = 50 (auswerten für Anfangsbedingung)
c 1 = 50 - 600 = -550Die Salzmenge beträgt
s[t] = 600 - 550e^(-t/100)) Nach 50 Minuten
beträgt die Salzmenge im Tank s[50] = 600 - 550*e^(-1/2)
s [50] ≈ 266,4 Pfund Salze Die vorhandene Menge, wenn t sehr groß wird, ist
s[unendlich] = 600 Pfund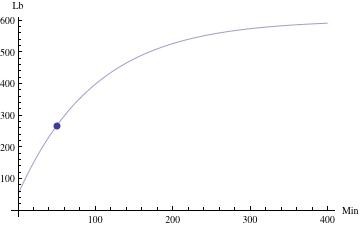
Verwandte Fragen
- Wie können wir Zwölftausend Zwölfhundert und Zwölf in Ziffern schreiben?
- Können Sie zeigen, dass die Summe einer irrationalen und einer rationalen Zahl immer eine irrationale Zahl ist?
- Was bedeutet Viereck?
- Was bedeutet Quotient?
- Wie finden Sie die Fläche eines Achtecks?
- Wie heißt ein zehnseitiges Objekt?
- Was bedeutet symmetrisch?
- Was ist eine "skalare" Größe? Bitte geben Sie Beispiele.