Когда сопротивление источника тока и внешнее сопротивление (нагрузка) определенной цепи становятся равными, как и почему рассеиваемая мощность максимальна? Какая в этом случае подача тока, максимальная или минимальная?

Вы должны быть немного осторожны в своих размышлениях об этом и в терминологии, которую вы используете для описания ситуации.

В двухконтактной линейной схеме, которую можно смоделировать с помощью источника постоянного напряжения питания (Vs) и постоянного импеданса источника (Rs), максимальная рассеиваемая мощность будет происходить, когда две клеммы закорочены . Рассеиваемая мощность будет равна
  max power = (Vs) ^ 2 / Rs.
Вся эта мощность рассеивается в импедансе источника, что часто не очень полезно. (Это может быть очень полезно в определенных ситуациях, когда рассеяние мощности нагрузки выше некоторого максимума может вызвать пожар, взрыв или другие неблагоприятные эффекты.)

Иногда нас интересует передача максимальной мощности от источника на сопротивление нагрузки (Rl). Это может иметь место, например, когда нагрузкой является антенна для радиопередачи. Когда полное сопротивление нагрузки линейно, уравнение, моделирующее мощность нагрузки, можно записать как
  мощность нагрузки = (Vs / (Rs + Rl)) ^ 2 * Rl = Vs ^ 2 * Rl / (Rs + Rl) ^ 2)

Проверка этого уравнения покажет, что когда Rl = 0, мощность нагрузки = 0. Мощность нагрузки также приближается к нулю, поскольку полное сопротивление нагрузки стремится к бесконечности. Между этими крайностями есть максимум. Мы можем найти эту точку, дифференцируя это выражение относительно Rl
  d (мощность нагрузки) / dRl = Vs ^ 2 * (Rs-Rl) / (Rs + Rl) ^ 3.
Это будет ноль, когда Rs = Rl. Таким образом, максимальная мощность нагрузки будет рассеиваться при сопротивление нагрузки = полное сопротивление источника . Стоит отметить, что равное количество мощности рассеивается импедансом источника.
В условиях максимальной мощности нагрузки подаваемый ток составляет половину максимального тока, доступного от источника . Это ни максимум, ни минимум. Ток цепи определяется как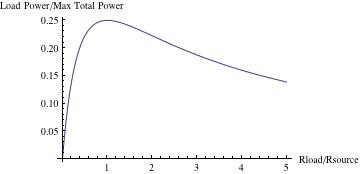
  ток = Vs / (Rs + Rl).
Очевидно, он будет максимальным, когда Rl = 0,
  максимальный ток = Vs / (Rs + 0) = Vs / Rs При условиях максимальной мощности нагрузки (Rl = Rs), это будет
  максимальный ток мощности нагрузки = Vs / (Rs + Rs) = Vs / (2 * Rs) = (1/2) * (максимальный ток)

Вышеприведенная математика применима к линейным цепям постоянного тока или к линейным цепям переменного тока, когда все импедансы являются действительными (без реактивных составляющих). Когда полное сопротивление источника содержит реактивную составляющую (как это часто бывает с импедансом переменного тока), максимальная мощность передается на нагрузку, которая является комплексно сопряженной величиной полного сопротивления источника.

При передаче электроэнергии переменного тока мы не заинтересованы в потере половины генерируемой мощности в системе передачи. Скорее, мы хотим , чтобы нагрузка использовалась как можно большей частью общей мощности. В этом случае используются трансформаторы, чтобы сделать кажущийся импеданс нагрузки как можно большим, поэтому полное сопротивление источника составляет пренебрежимо малую часть полного импеданса цепи.

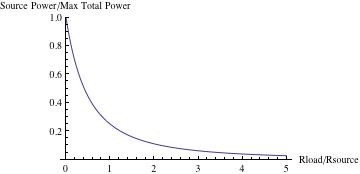
Эта кривая показывает, как рассеиваемая мощность в импедансе источника (Rs) уменьшается при увеличении импеданса нагрузки. Как указано в начале, максимальная общая рассеиваемая мощность происходит при нулевой нагрузке.