Lorsque la résistance de la source de courant et la résistance externe (charge) d'un certain circuit deviennent égales, comment et pourquoi la dissipation de puissance est-elle maximale ? Quelle est la fourniture de courant dans ce cas, est-elle maximale ou minimale ?

Vous devez être un peu prudent dans votre réflexion à ce sujet et dans la terminologie que vous utilisez pour décrire la situation.

Dans un circuit linéaire à deux bornes qui peut être modélisé par une source de tension d'alimentation constante (Vs) et une impédance de source constante (Rs), la dissipation de puissance maximale se produira lorsque les deux bornes sont en court - circuit . Cette puissance dissipée sera
  max power = (Vs)^2/Rs
Toute cette puissance est dissipée dans l'impédance de la source, souvent peu utile. (Cela peut être très utile dans certaines situations où la dissipation de puissance de charge au-dessus d'un certain maximum peut provoquer un incendie ou une explosion ou d'autres effets néfastes.)

Occasionnellement, nous sommes intéressés par le transfert de puissance maximale de la source à l'impédance de charge (Rl). Cela peut être le cas, par exemple, lorsque la charge est une antenne de transmission radio. Lorsque l'impédance de charge est linéaire, l'équation qui modélise la puissance de charge peut être écrite comme
  puissance de charge = (Vs/(Rs+Rl))^2*Rl = Vs^2*Rl/(Rs+Rl)^2)

Inspection de cette équation révélera que lorsque Rl=0, la puissance de charge = 0. La puissance de charge s'approche également de zéro lorsque l'impédance de charge tend vers l'infini. Entre ces extrêmes, il y a un maximum. Nous pouvons trouver ce point en différenciant cette expression par rapport à Rl
  d(puissance de charge)/dRl = Vs^2*(Rs-Rl)/(Rs+Rl)^3
Ce sera zéro lorsque Rs=Rl. Ainsi, la puissance de charge maximale sera dissipée lorsque impédance de charge = impédance de source . Il convient de noter qu'une quantité égale de puissance est dissipée par l'impédance de la source.
Dans des conditions de puissance de charge maximale, le courant fourni est la moitié du courant maximal disponible à partir de la source . Ce n'est ni maximum ni minimum. Le courant du circuit est donné par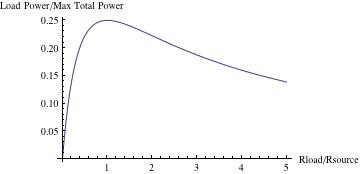
  courant = Vs/(Rs+Rl)
Il est clair qu'il sera maximum lorsque Rl=0
  courant max = Vs/(Rs+0) = Vs/Rs Aux conditions de puissance de charge max (Rl=Rs), ce sera le
  courant de puissance de charge max = Vs/(Rs+Rs) = Vs/(2*Rs) = (1/2)*(courant max)

Les calculs ci-dessus s'appliquent aux circuits CC linéaires ou aux circuits CA linéaires lorsque les impédances sont toutes réelles (sans composants réactifs). Lorsque l'impédance source contient une composante réactive (comme le font souvent les impédances AC), la puissance maximale est transférée à une charge qui est le conjugué complexe de l'impédance source.

Dans la transmission de courant alternatif, nous ne sommes pas intéressés à perdre la moitié de la puissance générée dans le système de transmission. Au contraire, nous voulons que la plus grande fraction possible de la puissance totale soit utilisée par la charge. Dans ce cas, des transformateurs sont utilisés pour rendre l'impédance de charge apparente aussi grande que possible, de sorte que l'impédance de la source représente une fraction négligeable de l'impédance totale du circuit.

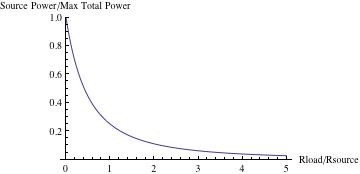
Cette courbe montre comment la dissipation de puissance dans l'impédance de source (Rs) diminue lorsque l'impédance de charge augmente. Comme indiqué au début, la dissipation de puissance totale maximale se produit lorsque la charge est nulle.