Écrivez l'équation du cercle contenant les points J(-6, 0), K(-3, 3) et L(0, 0). Afficher tous les travaux pour recevoir un crédit ?

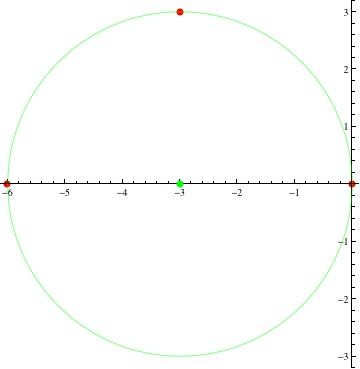
Un tracé des points révèle qu'ils sont des sommets d'un triangle rectangle isocèle. Le centre du cercle est le milieu du segment JL. Par inspection du graphique, ce point est (-3, 0). Le rayon est la distance du centre à l'un des points donnés. En inspectant le graphique, cette distance est de 3. L'équation est
  (xh)^2 + (yk)^2 = r^2, où (h, k) = (centre du cercle) = (-3, 0) et r =3.
  (x+3)^2 + y^2 = 9

---

N'oubliez pas de me créditer.