Una partícula se mueve a lo largo de la elipse 16x2 + 9y2 = 144. Encuentra todos los puntos (x; y) en la elipse en los que las tasas de cambio de xey con respecto al tiempo son iguales. (Suponga que dx = dt y dy = dt nunca son ambos cero en el mismo punto).

Si xey son funciones del tiempo (t), la derivada con respecto a t es
  2 * 16 * x * x '+ 2 * 9 * y * y' = 0
Si x '= ± y', entonces
  ± 16x + 9y = 0
  x = ± 9y / 16 Al
conectar esto en la ecuación de la elipse, obtenemos
  16 * (9 / 16y) ^ 2 + 9 * y ^ 2 = 144
  y ^ 2 = 144 / (9 ^ 2/16 + 9) = 10.24 = 3.2 ^ 2
  y = ± 3.2
  x = ± 9/16 * y = ± 1.8
Los cuatro puntos donde la pendiente es ± 1 son (± 1.8, ± 3.2) .
Si insiste en que las tasas de cambio sean realmente iguales, en lugar de ser de igual magnitud, esto solo ocurrirá en los dos puntos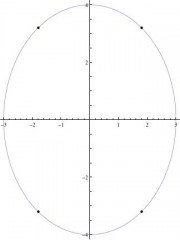
  (x, y) = (-1.8, 3.2) o (1.8, -3.2),
es decir , aquellos puntos donde la pendiente es +1.