sin (15 grados + x) + sin (45 grados-x) = 1 ¿Qué es x igual?

Sin (15 ° + x) + Sin (45 ° -x) = 1

Para comenzar a resolver este problema, debes usar la fórmula de suma a producto * para la suma de dos términos sinusoidales, donde sin (a) + sin (b) = 2sin [(a + b) / 2] cos [(ab ) / 2]. En este caso, el valor de "a" es 15 ° + x y el valor de "b" es 45 ° -x. Así que conectemos estos valores, ¿de acuerdo?

2sin [(15 ° + x) + (45 ° -x) / 2] cos [(15 ° + x) - (45 ° -x) / 2] = 1

Simplifica los términos dentro del paréntesis para los valores de seno y coseno. En (15 ° + x) + (45 ° -x), ya que los estamos sumando, podemos sumar directamente 15 con 45 para dar 60 grados. Y cuando sumamos x con x negativo, eso simplemente se cancela a 0, por lo que 60 + 0 sigue siendo 60. Y también estamos dividiendo toda la suma por 2, por lo que 60 dividido por 2 es igual a 30 grados.

2sin (30 °) cos [(15 ° + x) - (45 ° -x) / 2] = 1

Para (15 ° + x) - (45 ° -x), observe que se está realizando una resta. Vamos a distribuir eso a 45 grados y -x, así:

2 pecado (30 °) cos (15 ° + x-45 ° + x / 2) = 1

Observe cómo el 45 ° era originalmente positivo, pero se volvió negativo ya que le distribuimos el signo negativo al igual que el -x. Cuando agregas un negativo a algo que ya es negativo, se vuelve positivo, por lo que -x se convierte en positivo x. Ahora combinémoslos.

15 ° menos 45 ° se convierte en -30 °, y x + x se convierte en 2x, por lo que tenemos 2x - 30 °. Pero también estamos dividiendo toda la diferencia por 2, entonces (2x-30 °) / 2 = x-15 °. Ahora tenemos:

2 pecado (30 °) cos (x-15 °) = 1

Oh, mira, tenemos pecado (30 °) en la ecuación. Genial, veamos cuál es su valor en el círculo unitario.

Ahora que sabemos que el pecado (30) es 1/2, veamos nuestra ecuación.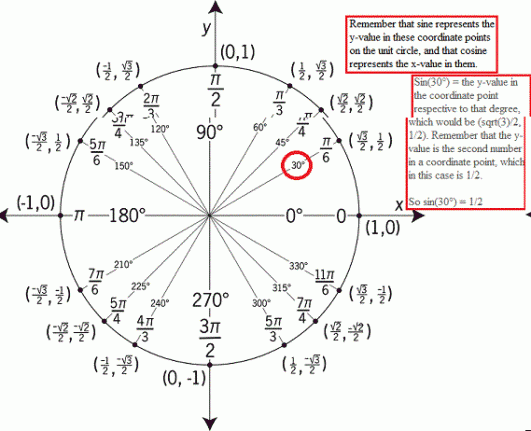

2 pecado (30 °) cos (x-15 °) = 1

Si sustituimos 1/2 por sin (30), también tenemos que multiplicarlo por 2, por lo que 1/2 * 2 es igual a 1. Y 1 por cos (x-15) es solo cos (x-15) , entonces tendremos:

cos (x-15) = 1

Ahora piense en esto, ¿qué grado debe tener el coseno para ser exactamente igual a 1? Recuerde que en un círculo unitario, el eje horizontal representa valores para x. El círculo se extiende hasta los valores de x -1 y 1 de izquierda a derecha, así como los valores de y -1 a 1 de abajo hacia arriba. Dado que el coseno se centra en los valores de x, preste atención al eje horizontal. ¿Dónde quedaría el coseno de algo igual a 1?

Respuesta: El coseno de algo es igual a 1 cuando ese algo está a 0 grados, o 360n grados. Verá, cuando tenemos cos (0) el punto de coordenadas que es respectivo a 0 grados es (1,0), y como sabemos que el coseno se centra en los valores de x, nuestra respuesta a cos (0) será 1. Entonces cos (0) = 1.

Por supuesto, siempre puedes agregarle 360, porque te dará la misma respuesta. El círculo unitario se expande a 360 grados completos, por lo que dar la vuelta a todo el círculo una vez lo llevará de regreso a donde comenzó. Entonces, otras opciones válidas podrían ser cos (360), cos (720), cos (1080), etc. (Ahí es donde entra 360n. La "n" representa cuántas veces agrega 360, por lo que tiene que ser un número entero ).

Muy bien, repasemos nuestra ecuación. Tenemos:

cos (x-15) = 1

Entonces, ¿qué valor debe tener x para obtener cos (0), ya que ahora sabemos que cos (0) = 1? Bueno, es fácil, simplemente establezca x - 15 igual a 0 y resuelva para x.

x - 15 = 0

x = 15 (añadido 15 a ambos lados)

Entonces x es igual a 15 grados. Pero recuerde, también puede agregar cualquier cantidad de 360 ​​porque le dará la misma respuesta, ya que agregar 360 grados significará que recorrerá todo el círculo de la unidad una vez y terminará de nuevo donde comenzó. Entonces la verdadera respuesta aquí es

x = 15 ° + 360 ° norte