Camille
¿Puede usted ayudar? Tengo una fórmula que se supone que debo usar, que es N = -x2-x = 41. Se supone que debo seleccionar algunos números para X, sustituirlos en la fórmula y ver si aparecen números primos. Entonces se supone que debo tratar de encontrar un número para X, que cuando lo sustituyo da como resultado
2 Respuestas
Clementina
Eche un vistazo a la imagen para ver el valor de su fórmula para varios valores de x diferentes.
Para x = 0 , N = - (0) 2 - (0) + 41 = -0-0 + 41 = 41 .
Da la casualidad de que 41 es un número primo . Puede verificar dividiendo entre primos impares menores que 7, es decir, 3 o 5.
Para x = 1 , N = - (1) 2 - (1) + 41 = -1-1 + 41 = 39 .
39 es un número compuesto , siendo el producto de 3 por 13.
_____
Para verificar que un número sea primordial, solo necesita dividir por números primos hasta la raíz cuadrada del número. 7 2 = 49, por lo que todos los valores que produce esta fórmula requerirán probar solo con 3 y 5. Cualquier valor par que no sea 2 no es primo. (11, 29, 41 son primos; 21 = 3 * 7, 35 = 5 * 7, 39 = 3 * 13)
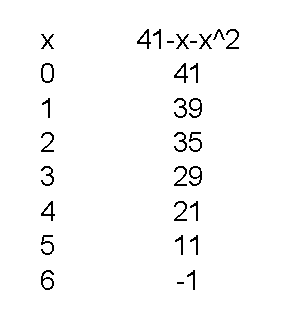
Wilburn
En primer lugar, tiene la fórmula incorrecta. El primer término no es negativo, aunque honestamente no haría una diferencia ya que cualquier número negativo al cuadrado es positivo. Oddman te dio información incorrecta, porque usó la ecuación -1 - 1 + 41 = 39. Como no puedes elevar al cuadrado -1 y obtener -1, tu ecuación en realidad sería 1 - 1 + 41 = 41 ya que 1 - 1 = 0 y 0 + 41 = 41. He usado esta fórmula sustituyendo x por varios números pares e impares y hasta ahora he obtenido cualquier cosa menos números primos.
Preguntas similares
- ¿Cómo convierto kg en piedra?
- ¿Cómo calcular el porcentaje?
- ¿Cómo calcular el volumen de un cilindro?
- ¿Cómo calcular el porcentaje de pendiente?
- ¿Qué es un poliedro?
- ¿Cómo llegaron a existir los números aritméticos?
- ¿Qué es un ábaco?
- ¿Cuál es el porcentaje de la población mundial que es zurda?