Ellis
Inicialmente, se disuelven 50 libras de sales en un tanque grande que tiene 300 galones de agua. ¿Se bombea una solución de salmuera al tanque a una velocidad de 3 gal / min y luego se bombea una solución bien agitada a la misma velocidad?
1 Respuestas
Emelia
Suponga que la cantidad total de sales en el tanque es s [t] libras, donde t es el tiempo en minutos. Se nos dice que
s [0] = 50 libras
La tasa de aumento de s [t] es
(3 gal / min) * (2 lb / gal) = 6 lb / min
La tasa de disminución de s [t] (en libras por minuto) es
s / (300 gal) * (3 gal / min)
Expresando estas relaciones usando una ecuación diferencial, tenemos
s '[t] = 6 - (1/100) * s,
s [0] = 50
Reconocemos que la solución a esta ecuación lineal no homogénea con coeficientes constantes será de la forma
s [t] = c 1 e ^ (a * t) + c 0 para algunos valores de ay constantes c n .
Sustituyendo esto en la ecuación diferencial anterior y haciendo coincidir los coeficientes, obtenemos
c 1 * a * e ^ (a * t) = 6 - (1/100) * c 1 * e ^ (a ^ t) - (1/100 ) * c 0 c 1 * a = - (1/100) * c 1 (igualar los coeficientes de e ^ (a * t))
a = -1/100 0 = 6 - (1/100) * c 0 (igualar constantes)
c 0 = 600 c 1 * e ^ (- 0/100) + 600 = 50 (evaluar la condición inicial)
c 1 = 50 - 600 = -550La cantidad de sal es
s [t] = 600 - 550e ^ (- t / 100)) Después de 50 minutos, la cantidad de sal en el tanque será
s [50] = 600 - 550 * e ^ (- 1/2)
s [50] ≈ 266.4 libras de sales La cantidad presente cuando t se vuelve muy grande será
s [infinito] = 600 libras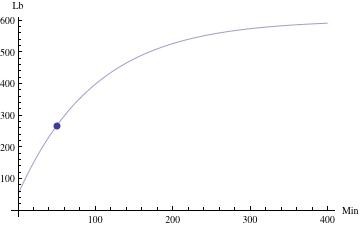
Preguntas similares
- ¿Cómo convierto kg en piedra?
- ¿Cómo calcular el porcentaje?
- ¿Cómo calcular el volumen de un cilindro?
- ¿Cómo calcular el porcentaje de pendiente?
- ¿Qué es un poliedro?
- ¿Cómo llegaron a existir los números aritméticos?
- ¿Qué es un ábaco?
- ¿Cuál es el porcentaje de la población mundial que es zurda?