Wie groß ist der Dellenwinkel bei einem sternförmigen Polygon mit 8 Punkten und einem Spitzenwinkel von 200?

Unter der Annahme eines regelmäßigen Polygons bestehend aus 8 Punkten und 8 "Beulen" scheint die Figur eine der folgenden zu sein. (Der 200°-Winkel ist mit einem Bogen gekennzeichnet.)
So oder so scheint die "Delle" sehr nach einem "Punkt" auszusehen.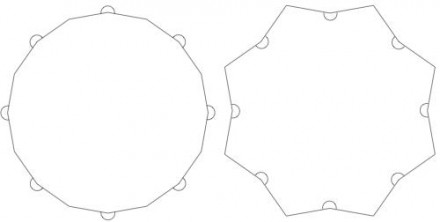
Wenn Beulen und Spitzen als Innenwinkel gemessen werden (wie rechts), beträgt die Summe eines Beulen-Punkte-Paares 14/8*180° = 315°. Somit beträgt ein "Beulen"-Winkel 115°.
Wenn Dellen und Punkte außen gemessen werden (wie links), beträgt die entsprechende Summe jedes Dellen-Punkte-Paares 360°(1+1/8) = 405°. Somit beträgt ein "Beulen"-Winkel 205°.
Der Konkavwinkel in der Abbildung rechts beträgt natürlich 360° - 200° = 160°.

Vielleicht meinen Sie, dass der Spitzenwinkel 20° beträgt. Dann würde die Figur so aussehen.
Der innere Dellenwinkel beträgt 315° - 20° = 295°, also der äußere Dellenwinkel 65° .