17 Antworten
Blaise
Ich brauche eine Formel zur Berechnung der Abmessungen von 2 Seiten eines Dreiecks. Ich kenne die Grade aller 3 Seiten des Dreiecks. 90, 30, 60. Die Hypotenuse ist 36".
Bitte helfen Sie!Beulah
Wenn erster Winkel x
zweiter Winkel ist 2x
3. Winkel ist ???
Und alle drei Winkel müssen sich zur Summe aller Winkel aller Dreiecke addierenHarmonie
Der zweite Winkel eines Dreiecks ist 15 Grad größer als der erste. Der dritte Winkel ist 23 Grad kleiner als der erste. Was ist das genaue Maß aller drei Winkel? HilfeKatrine
Nehmen wir an, Sie haben 40 und 50, dann addieren Sie sie und die Antwort wäre 90 für den letzten Schritt, dann ziehen Sie 90 von 180 und 180 ab, weil 180 die Länge des Dreiecks ist, egal was passiert!Sandrine
Nun, Sie müssen wissen, was der Winkel eines vollen Dreiecks ist. Finden Sie dann heraus, wie viel von dem Dreieck fehlt. Sie können diese beiden subtrahieren, um herauszufinden, wie viel des Winkels des Dreiecks mit dieser Methode auch tatsächlich vorhanden ist.Philipp
180 Grad entspricht einem Dreieck. Wenn ein Winkel 30, sagen wir, und ein anderer 70 ist, so tun, als ob, was ist dann noch erforderlich, um 180 zu erreichen? In diesem gefälschten Fall wäre es 80, was bedeuten würde, dass der verbleibende Winkel 80 Grad beträgt.Frieda
Verwenden Sie die Formel a + b + c = 180 Grad Ich hatte die gleiche Frage und das hat mir mein Lehrer gesagt. Es funktioniert wirklich, das kann ich garantieren!Elliott
Sie nehmen die höchste Winkelzahl und subtrahieren die niedrigere Zahl von der höheren, damit Ihre Antwort das ist, was Sie auch immer von der Antwort abgezogen haben!!! Wie einfach war das?Dedrick
Wie findet man die fehlenden Winkel eines Dreiecks mit nur einem gegebenen Winkel? Die Basis ist 16" und die Höhe 4"Kacie
Das Maß des zweiten Winkels eines Dreiecks beträgt 5 Grad mehr als das Vierfache des ersten und das Maß des dritten Winkels beträgt 27 Grad weniger als das Dreifache des zweiten Winkels. Finden Sie das Maß für jeden Winkel.Haley
Sie können so ziemlich jeden Winkel mit trigonometrischen Funktionen berechnen. Diese Funktionen arbeiten mit rechtwinkligen Dreiecken, liefern aber Antworten für jedes Dreieck, das in zwei rechtwinklige Dreiecke zerlegt werden kann. Zur
Illustration:
Der Sinus des Winkels a ist ein Verhältnis der Länge der Gegenseite zur Länge der Hypotenuse.
Der Kosinus des Winkels a ist ein Verhältnis der Länge der angrenzenden Seite zur Länge der Hypotenuse.
Die Tangente des Winkels a ist ein Verhältnis der Länge der gegenüberliegenden Seite zur Länge der benachbarten Seite.
Nur für den Fall, dass Sie nicht wissen, dass Verhältnis geteilt durch ist.
Wenn wir die Länge von zwei beliebigen Seiten des Dreiecks kennen, können wir entweder den Sinus, den Kosinus oder den Tangens berechnen und daraus den Winkel bestimmen.
Da die Summe der drei Winkel eines Dreiecks 180 o betragen muss und ein Winkel eines rechtwinkligen Dreiecks immer 90 o beträgt, können wir den dritten Winkel berechnen.
Nehmen wir als Beispiel an, dass die angrenzende Seite 6 Zoll und die Hypotenuse 8 Zoll beträgt, wir können den Kosinus des Winkels a als 6/8 = 0,750 berechnen. Wenn wir die trigonometrischen Tabellen oder einen ausgefallenen Taschenrechner überprüfen, sehen wir, dass .750 der Kosinus des Winkels 41.41 o ist . Wenn Sie keinen ausgefallenen Taschenrechner haben und die Tabellen verwenden, müssen Sie möglicherweise interpolieren. (Aber das ist eine andere Geschichte).
Da der unbekannte Winkel = 180-(90+41,41) ist, sind die drei Winkel 41,41, 90 und 48,59.
Es gibt noch andere trignometrische Funktionen, aber Sinus, Cosinus und Tangens werden den Großteil der Arbeit erledigen.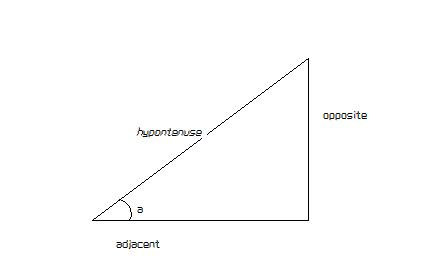
Da ist ein
Die drei Winkel sind
x
2x
2x + 10
Sie müssen sich addieren zu 180
x + 2x + 2x + 10 = 180
5x + 10 = 180
5x = 170
x = 34 (Winkel1
2x = 68(Winkel2)
y=2x+10
y = 2(34) + 10
y = 78 (Winkel3)
34 + 68 + 78 = 180.
Nedra
Alle Winkel eines Dreiecks addieren sich zu 180 Grad, egal wie groß das Dreieck ist, sagen wir, 1 Winkel ist 50 Grad, ein anderer 50 Grad und was ist dann die letzte 1? Es müssten 80 Grad sein --- 50+50+_=180? 50+50+80=180.Kadin
Normalerweise beträgt in jedem Dreieck die Summe der drei Winkel 180. Sie kennen bereits zwei Winkel. Sie müssen den fehlenden Winkel finden. Betrachten Sie das Dreieck ABC. In diesem Dreieck sind A, B die bekannten Winkel. Wir müssen den Winkel C finden. Die Summe der drei Winkel ist 180. also A+B+C = 180, C = 180 - (A+B)Filiberto
Sie werden immer eine Länge von 180 für Ihr Dreieck haben und wenn Sie wissen, dass alles von dort aus fließt, weil sagen, Ihre anderen beiden Winkel sind 30 und 20, was Ihnen 50 ergibt, dann ziehen Sie 50 von 180 ab und erhalten 130, was Ihnen fehlt Winkel, ich hoffe, das hilft in irgendeiner Weise :)Ewald
Es gibt einige Formeln, mit denen Sie die Dreiecksgrade mithilfe der Trigonmetrie berechnen können.
A=Winkel 1
b = Winkel 2
c = Winkel 3
A = Seite 1
B = Seite 2
C = Seite 3
a² = b²+c² - 2bc weil A
c² = a² + b² - 2ab weil C
Sin A/a =Sin C/ c = Sin B/b
Angrenzend bedeutet neben- oder nebeneinander. Wie benachbarte Winkel oder benachbarte Seiten. Hypotenuse ist die gegenüberliegende Seite des 90-Grad-Winkels in einem rechtwinkligen Dreieck. Wenn Sie beispielsweise zwei Linien im rechten Winkel zeichnen, ist die dritte Linie, die die beiden verbindet, die Hypontenuse.Alec
Sie addieren die angegebenen Winkel und subtrahieren die Summe dieser beiden Zahlen von 180 Grad, denn egal, was das Dreieck ergibt, ergibt 180 ... Und was immer Sie erhalten, ist die Menge der fehlenden Grade.
Und dann bist du fertig.
Ich hoffe, das hat geholfen.
Verwandte Fragen
- Was ist ein Polygon?
- Wie finde ich Summen von Winkelmaßen?
- Wie heißt eine ovale 3D-Form?
- Mein 30 Jahre alter Badezimmer-Deckenventilator hat einen 10 Zoll Durchmesser (rund) in meinen Dachboden. Alle Ersatzlüfter haben quadratische Halterungen. Ich kann die Decke nicht auf den quadratischen Ventilator zuschneiden. Was kann ich tun?
- Wie finde ich die geometrischen Abmessungen eines 5-seitigen Sterns?
- Wie lautet die Formel für das Volumen eines rechteckigen Festkörpers?
- Wie können Koordinaten in einem Gitter eine Linie beschreiben, die doppelt so lang ist wie eine andere Linie?
- Wie sieht eine sechseckige Pyramide aus?