Wie finden Sie die Seitenlängen eines regelmäßigen Sechsecks, wenn es 10 % eines 8,5x11-Papiers einnimmt?

Nehmen wir also an, dies war das Sechseck, das sich auf einem 8,5 x 11-Papier befand und 10% davon bedeckte:

Das würde bedeuten, dass die Fläche des Sechsecks 10 % der Fläche eines 8,5x11-Papiers beträgt, was auch bedeutet, dass die Fläche des Papiers 10x größer ist als die des Sechsecks. Wir müssen zunächst die Flächen beider Formen berechnen.

Die Fläche eines 8,5x11-Papiers muss die Formel für die Fläche eines Rechtecks ​​verwenden: Länge mal Breite.

A (Papier) = 8,5 * 11 = 93,5 Zoll^2.

Jetzt haben wir die Fläche des Papiers. Denken Sie daran, dass das Problem besagt, dass das Sechseck 10 % des Papiers bedeckt und daher 1/10 der Fläche des Papiers hat. So:

A(Sechseck) = A(Papier)/10

Wir wissen bereits, was die Fläche des Papiers ist.

A(Sechseck) = 93,5/10

= 9,35 Zoll^2

Jetzt kennen wir die Flächen beider Formen und müssen die Seitenlängen herausfinden. Würden Sie zustimmen, dass ein Sechseck wie 6 gleichseitige Dreiecke kombiniert aussieht? Schau dir das an:

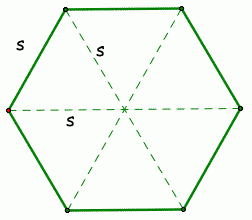
Ignoriere die "s"-Symbole für den Moment.

Denken Sie daran, dass die Fläche eines gleichseitigen Dreiecks Basis mal Höhe geteilt durch 2 ist.

A(Dreieck) = bh/2

In diesem Sechseck haben wir jedoch sechs dieser Dreiecke. Wir können die Fläche des Sechsecks verwenden, um die Fläche nur eines gleichseitigen Dreiecks zu ermitteln und diese mit 6 zu multiplizieren und dann unsere Seitenlängen zu ermitteln.

A(Dreieck) = A(Sechseck)/6

A(Dreieck) = 9,35/6

A (Dreieck) = bh / 2 = 1,558 Zoll ^ 2 (ungefähr so ​​viel)

Von diesem Punkt an wird ein wenig Trigonometrie mit rechtwinkligen Dreiecken benötigt.

Dies sollte ein gleichseitiges Dreieck sein, aber ich habe es irgendwie schnell gezeichnet, also verzeihen Sie meine schlechten künstlerischen Fähigkeiten.

Jedenfalls habe ich in der Mitte des Dreiecks eine Linie gezeichnet, die die Höhe darstellt. Aber vergiss das erstmal. Wenn in der Trigonometrie eine solche Form mit einer Linie in der Mitte auftrat, gab es immer einen Winkel von 30, 60 und 90 Grad. Ich habe das auf die Form beschriftet. Und für die dem Winkel gegenüberliegenden Seiten repräsentierten sie eine gewisse Länge.

30-Grad-Winkel werden als "a" dargestellt.

60-Grad-Winkel werden als "a" multipliziert mit "sqrt(3)" dargestellt.

90-Grad-Winkel werden als "a" multipliziert mit 2 dargestellt.

Kommen wir zurück zur Linie in der Mitte des Dreiecks. Das repräsentiert die Höhe, wie ich bereits erwähnt habe. Aber rate mal was? Es stellt auch ein * sqrt(3) dar. Wir können dies also als Wert für die Höhe wieder in unsere Gleichung für das Dreieck verwenden.

A(Dreieck) = 1,558 = [b * a * sqrt(3)]/2

Jetzt finden Sie b. Beachten Sie, dass "a", das dem 30-Grad-Winkel entgegengesetzt ist, nur die linke Hälfte der Seitenlänge der Basis darstellt. Da es nur die Hälfte misst, müssen wir es mit 2 multiplizieren, um die Länge der gesamten Basis des Dreiecks zu erhalten, was 2a ergibt. Also b = 2a.

A(Dreieck) = 1,558 = [2a * a * sqrt(3)]/2

Von hier aus wird es VIEL einfacher, vertrau mir. Vereinfachen Sie die Gleichung, um nach a aufzulösen.

1,558 = [2a^2 * Quadrat(3)]/2

1,558 = a^2 * sqrt(3) (die 2 vor a^2 hebt sich auf, indem die 2 die gesamte rechte Seite der Gleichung teilt)

1,558/sqrt(3) = a^2

a^2 = 0,9

Ziehe die Quadratwurzel von beiden Seiten.

a = 0,948

Jetzt, da wir wissen, was a ist, gehen wir ein wenig zurück. Wie schon gesagt, b = 2a, richtig? Nun, rate mal, was b auch repräsentiert? Die Seitenlänge eines Sechsecks!

Ja, es ist eine Seitenlänge des gleichseitigen Dreiecks, aber ein Sechseck besteht aus 6 gleichseitigen Dreiecken, also haben beide die gleiche Seitenlänge.

Seitenlänge = 2a

Setzen Sie den Wert für a ein.

Seitenlänge = 2 (0,948) = 1,896 Zoll.