Wie berechnet man die Fläche eines Sechsecks?

Es gibt drei Möglichkeiten, die Fläche eines Sechsecks zu berechnen. Die Formel dafür lässt sich am einfachsten verstehen, wenn man erkennt, dass ein regelmäßiges Sechseck aus sechs gleichseitigen Dreiecken besteht. Die Formel wird also aus der Formel entwickelt, um die Fläche eines gleichseitigen Dreiecks zu finden.

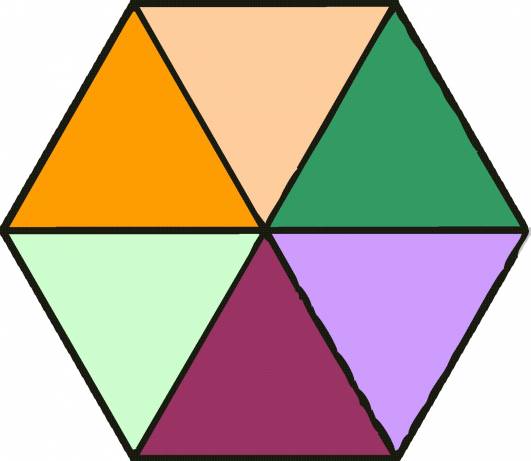
Die erste Formel zum Bestimmen der Fläche eines Sechsecks ist Fläche
= (3√3 s ² )/2 wobei 's' die Länge einer Seite des regelmäßigen Sechsecks ist. Sie müssen die Länge der Seite angeben und 's' durch diese Zahl ersetzen. Wenn der Wert von 's' beispielsweise 9 cm beträgt, wäre Ihre schrittweise Arbeit für die Gleichung:

(3√3 x 9 ² )/2 = (3√3 x
81)/2 = (243√3)/2 = 420,8/2 = 210,4 cm ²

Andere Formeln beinhalten: Fläche = 1/2 x Umfang x Apothem

Apothem = eine Linie von der Mitte eines regelmäßigen Vielecks im rechten
Winkel zu einer seiner Seiten

Umfang = die durchgehende Linie, die die Grenze einer geschlossenen
geometrischen Figur bildet.

Fläche = Die Ausdehnung innerhalb einer Form.

Wenn der Umfang 60 cm beträgt und das Apothem 5√3 beträgt, würden Sie Folgendes berechnen:

◦ 1/2 x 60 cm x 5√3 cm =

◦ 30 x 5√3 cm =

◦ 150√3 cm =

259,8 cm ²

So berechnen Sie ein unregelmäßiges Sechseck :

Wenn Sie die Eckpunkte des Hexagons erhalten, sollten Sie ein Diagramm mit zwei Spalten und sieben Zeilen erstellen, wobei jede Zeile mit den sechs Punkten und jede Spalte mit x oder y der Punkte gekennzeichnet ist. Wiederholen Sie die Koordinaten des ersten Punktes am Ende der Liste.

Scheitelpunkte = jeder Winkelpunkt eines Polygons, Polyeders oder einer anderen Figur.

Multiplizieren Sie dann die x-Koordinaten jedes Punktes mit der nächsten y-Koordinate und addieren Sie dann die Ergebnisse.

Dann multiplizieren Sie die y-Koordinaten jedes Punktes mit der nächsten x-Koordinate und addieren dann die Ergebnisse.

Subtrahieren Sie dann den zweiten Koordinatensatz vom ersten Koordinatensatz.

Dann dividiere diese Differenz durch zwei.