Wenn zwei Eckpunkte von und gleichseitiges Dreieck (-4, -3) und (4, 1) sind, den verbleibenden Eckpunkt finden?

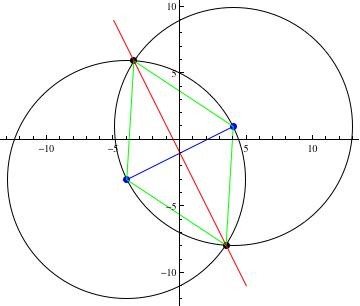
Es wird zwei solcher Scheitelpunkte geben. Einer befindet sich im zweiten Quadranten und einer im vierten Quadranten. Sie liegen auf der Mittelsenkrechten der Linie zwischen den gegebenen Punkten und werden an den Schnittpunkten von Kreisen gefunden, die an jedem Punkt mit einem Radius gleich dem Abstand zwischen den Punkten zentriert sind. (Siehe Abbildung unten.)

Der Abstand zwischen den gegebenen Punkten ist
  r = √((-4-4)^2 + (-3-1)^2) = √(64+16) = √80

Der Kreis zentriert bei (-4, -3) hat die Gleichung
  (x + 4)^2 + (y + 3)^2 = 80
  x^2 + 8x + 16 + y^2 + 6y + 9 = 80 (Erweiterung der Gleichung. Nennen Sie dies [1])

Der Kreis um (4, 1) hat die Gleichung
  (x - 4)^2 + (y - 1)^2 = 80
  x^2 - 8x + 16 + y^2 - 2y + 1 = 80 (Erweiterung der Gleichung. Nennen Sie dies [2])

Wir können [1] = [2] setzen und nach y auflösen.
  x^2 + 8x + 16 + y^2 + 6y + 9 = 80 = x^2 - 8x + 16 + y^2 - 2y + 1
  8x + 6y + 9 = -8x - 2y + 1 (subtrahiere x^2 +16+y^2 von beiden Seiten)
  6y = -16x - 2y - 8 (subtrahiere 8x+9 von beiden Seiten)
  8y = -16x - 8 (addiere 2y)
  y = -2x - 1 (dividiere durch 8. Das ist die Gleichung der roten Linie Nennen Sie dies [3])

Wir können [3] in [1] einsetzen und nach x auflösen. In der Abbildung ergibt dies die x-Koordinate der Schnittpunkte der roten Linie und des unteren Kreises.
  x^2 + 8x + 16 + ( -2x - 1 )^2 + 6( -2x - 1 ) + 9 = 80
  x^2 + 8x + 16 + 4x^2 + 4x + 1 - 12x - 6 + 9 = 80 (Klammern entfernen)
  5x^2 + 20 = 80 (Terme sammeln)
  5x^2 = 60 (Subtrahieren 20)
  x^2 = 12 (dividiere durch 5)
  x = ±2√3     ( ziehe die Quadratwurzel)

Dieses Ergebnis in [3] können wir verwenden, um die entsprechenden Werte von y zu finden. (Positives Vorzeichen zuerst.)
  y = -2(2√3) - 1 = -4√(3) - 1
Die Ecke des Quadranten IV ist (2√3, -4√(3) - 1) .

  y = -2(-2√3) - 1 = 4√(3) - 1
Die Ecke des Quadranten II ist (-2√3, 4√(3) - 1) .