Erklären Sie, warum die Winkelpaare, die aus zwei Geraden und einer Transversalen gebildet werden, Ihrer Meinung nach verwandt sind. Warum könnte es hilfreich sein, sie als zusammengehörende Winkel und nicht als unabhängige Winkel zu identifizieren?

Sie sind in vielerlei Hinsicht verwandt.

Eine Transversale wird benötigt, um Winkelpaare zu bilden, wie in diesem Bild.

Die Transversale ist eindeutig die Linie, die im Vergleich zu den anderen beiden Linien hauptsächlich vertikal ist. Ohne sie könnten keine Winkelpaare gebildet werden. Sie können jedoch immer noch ohne Transversal hergestellt werden, wie in diesem Bild.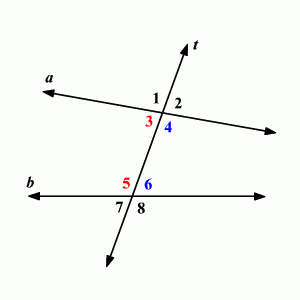

Bild 1 zeigt jedoch mehr darüber, wie eine Transversale mit Winkelpaaren zusammenhängt, da sie benötigt wird, um sie tatsächlich zu erstellen!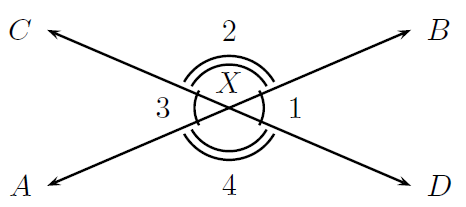

Warum könnte es hilfreich sein, sie als zusammengehörende Winkel und nicht als unabhängige Winkel zu identifizieren?

Schauen wir uns das zweite Bild an. Es zeigt, dass die Winkel 1 und 3 gleich sind (durch Zeichnen eines kleinen Bogens neben jedem Winkel) sowie die Winkel 2 und 4 gleich sind (durch Zeichnen von zwei kleinen Bögen neben jedem Winkel). Wenn wir gebeten würden, eine genaue Winkelgradmessung herauszufinden, würde uns die Verwendung von Winkelpaaren hier 50% der Arbeit sparen. Nehmen wir an, wir haben die Gradmessung für Winkel 1 herausgefunden. Aufgrund einer Winkelpaarregel können wir sagen, dass Winkel 3 die gleiche Gradzahl hat, was uns bereits 25% der Gesamtarbeit spart. Wenn wir das gleiche mit den Winkeln 2 und 4 machen, werden weitere 25% der Gesamtarbeit eingespart. Aus diesem Grund ist es hilfreich, Winkelpaare als zusammengehörende Winkel und nicht als unabhängige Winkel zu identifizieren.

Eine Transversale ist eine einzelne Linie, die zwei oder mehr andere Linien kreuzt. Diese Linien können parallel sein, müssen es aber nicht. Dies ist eines der grundlegenden Konzepte der Geometrie.

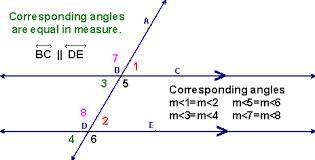
Die Transversale bildet einen Winkel aus ansonsten im Wesentlichen zwei Geraden. Wenn dies geschieht, werden die gebildeten Winkel in Paare unterteilt: Vertikale Winkel, entsprechende Winkel, abwechselnde Innenwinkel, abwechselnde Außenwinkel und aufeinanderfolgende Innenwinkel.

Die einzige andere Möglichkeit, wie zwei Geraden ohne Hilfe einer Transversale Winkel bilden könnten, besteht darin, dass sich die beiden Geraden irgendwann kreuzen.

Es ist hilfreich, Winkel paarweise und nicht unabhängig voneinander zu identifizieren, da wir wissen, dass eine Gruppe von Winkeln, die durch eine Transversale erstellt wird, Eigenschaften teilt, die ihre Identifizierung erleichtern. Zum Beispiel bilden die beiden Winkel 7 und 1 im obigen Bild zusammen eine gerade Linie - was uns sagt, dass die Summe ihrer Messungen 180 Grad betragen muss.