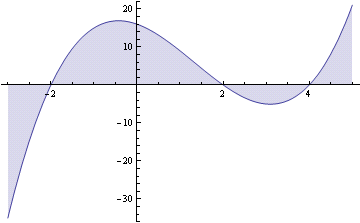
Найти площадь, ограниченную осью X и кривой Y = (x-4) (x-2) (x + 2)?

Площадь, ограниченная интересующей областью, будет определенным интегралом этого выражения по интересующей области. Интеграл от
y = 16 - 4x - 4x ^ 2 + x ^ 3

равен
g [x] = Integral [y] = 16x - 2x ^ 2 - (4x ^ 3) / 3 + x ^ 4/4

Если область интерес равен x = {-2, 2}, площадь оценивается как
g [2] - g [-2] = (52/3 - (-76/3)) = 128/3.

Пожалуйста, взгляните на картинку.