Wenn der Widerstand der Stromquelle und der externe Widerstand (Last) einer bestimmten Schaltung gleich werden, wie und warum ist dann die Verlustleistung maximal? Was ist in diesem Fall die Stromzufuhr, ist sie maximal oder minimal?

Sie müssen ein wenig vorsichtig sein, wenn Sie darüber nachdenken und in der Terminologie, die Sie verwenden, um die Situation zu beschreiben.

In einer linearen Schaltung mit zwei Anschlüssen, die durch eine konstante Versorgungsspannungsquelle (Vs) und eine konstante Quellenimpedanz (Rs) modelliert werden kann, tritt die maximale Verlustleistung auf, wenn die beiden Anschlüsse kurzgeschlossen sind . Diese Verlustleistung beträgt
  max. Leistung = (Vs) ^ 2 / Rs
Diese gesamte Leistung wird in der Quellimpedanz abgeführt, was oft nicht sehr nützlich ist. (Dies kann in bestimmten Situationen sehr nützlich sein, in denen eine Lastverlustleistung über einem bestimmten Maximum zu einem Brand, einer Explosion oder anderen schädlichen Auswirkungen führen kann.)

Gelegentlich sind wir daran interessiert, die maximale Leistung von der Quelle auf die Lastimpedanz (Rl) zu übertragen. Dies kann beispielsweise der Fall sein, wenn die Last eine Antenne für die Funkübertragung ist. Wenn die Lastimpedanz linear ist, kann die Gleichung, die die
  Lastleistung modelliert, geschrieben werden als Lastleistung = (Vs/(Rs+Rl))^2*Rl = Vs^2*Rl/(Rs+Rl)^2)

Inspektion dieser Gleichung zeigt, dass, wenn R1 = 0, Lastleistung = 0 ist. Die Lastleistung nähert sich auch Null, wenn die Lastimpedanz gegen Unendlich geht. Zwischen diesen Extremen gibt es ein Maximum. Wir können diesen Punkt finden, indem wir diesen Ausdruck nach Rl
  d( Lastleistung )/dRl = Vs^2*(Rs-Rl)/(Rs+Rl)^3
differenzieren. Dies ist null, wenn Rs=Rl. Somit wird die maximale Lastleistung abgeführt, wenn Lastimpedanz = Quellimpedanz . Es ist erwähnenswert, dass eine gleiche Menge an Leistung von der Quellimpedanz abgeleitet wird.
Unter Bedingungen maximaler Lastleistung ist der gelieferte Strom die Hälfte des maximalen Stroms, der von der Quelle verfügbar ist . Es ist weder ein Maximum noch ein Minimum. Der Strom des Schaltkreises wird durch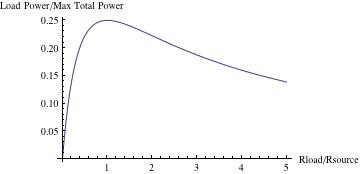
  Strom = Vs/(Rs+Rl) gegeben
. Dieser ist eindeutig maximal, wenn Rl=0
  max. Strom = Vs/(Rs+0) = Vs/Rs Bei maximalen Lastleistungsbedingungen (Rl=Rs) Dies ist der
  maximale Laststrom = Vs/(Rs+Rs) = Vs/(2*Rs) = (1/2)*(maximaler Strom)

Die obige Mathematik gilt für lineare Gleichstromkreise oder für lineare Wechselstromkreise, wenn alle Impedanzen real sind (ohne reaktive Komponenten). Wenn die Quellimpedanz eine reaktive Komponente enthält (wie dies bei Wechselstromimpedanzen häufig der Fall ist), wird die maximale Leistung an eine Last übertragen, die die komplex Konjugierte der Quellimpedanz ist.

Bei der Wechselstromübertragung geht es uns nicht darum, die Hälfte der erzeugten Leistung im Übertragungsnetz zu verlieren. Vielmehr möchten wir, dass der größtmögliche Anteil der Gesamtleistung von der Last verwendet wird. In diesem Fall werden Transformatoren verwendet, um die scheinbare Lastimpedanz so groß wie möglich zu machen, so dass die Quellenimpedanz einen vernachlässigbar kleinen Bruchteil der gesamten Schaltungsimpedanz darstellt.

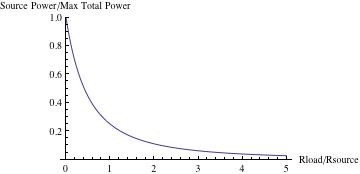
Diese Kurve zeigt, wie die Verlustleistung in der Quellimpedanz (Rs) mit steigender Lastimpedanz sinkt. Wie eingangs erwähnt, tritt die maximale Gesamtverlustleistung auf, wenn die Last Null ist.