Schreiben Sie die Gleichung des Kreises, der die Punkte J(-6, 0) enthält, K(-3, 3) und L(0, 0). Alle Arbeiten anzeigen, um eine Gutschrift zu erhalten?

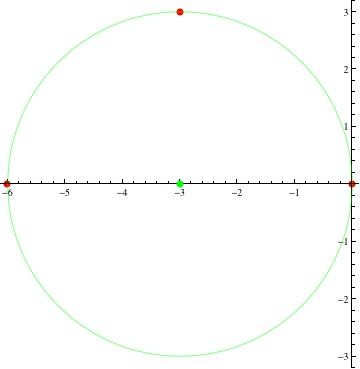
Ein Plot der Punkte zeigt, dass sie Eckpunkte eines gleichschenkligen rechtwinkligen Dreiecks sind. Der Mittelpunkt des Kreises ist der Mittelpunkt des Segments JL. Bei Betrachtung des Graphen ist dieser Punkt (-3, 0). Der Radius ist der Abstand vom Mittelpunkt zu einem der angegebenen Punkte. Nach Betrachtung des Graphen beträgt dieser Abstand 3. Die Gleichung ist
  (xh)^2 + (yk)^2 = r^2, wobei (h, k) = (Kreismitte) = (-3, 0) und r =3.
  (x+3)^2 + y^2 = 9

---

Vergessen Sie nicht, mir Kredit zu geben.